Electric potential difference
The ratio of the work done in taking a test charge from one point to another in an electric field to the test charge is called the potential difference between the points.
If the test charge is q₀, then the work done in taking it from point (b) to (a) is W.
Then potential difference between (a) and (b) is
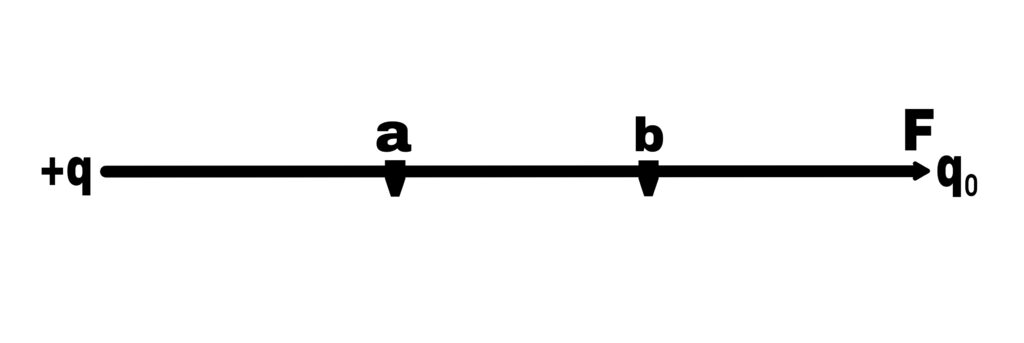
Va – Vb = W/q₀
Potential difference is a scalar quantity.
The other unit of potential difference is volt.
1 volt = 1 joule / coulomb
That is,
If 1 joule / coulomb of work has to be done in taking a test charge from one point to another in an electric field, then the potential difference between those points will be 1 volt.
If B is also at infinity then,
Va-V∞ = (W∞→a)/q₀
Va = (W∞→a)q₀
Where,
Va is the potential at point a and it is defined as follows.
Electric potential
If,
q₀=1
Va = W∞→a
The work done to bring a unit charge from infinity to a point is its potential at that point.
Unit and dimensions of potential
Unit
Joule / Coulomb = Volte
Dimension
[ML²T⁻²] / [AT]
[ML²T⁻³A⁻¹]
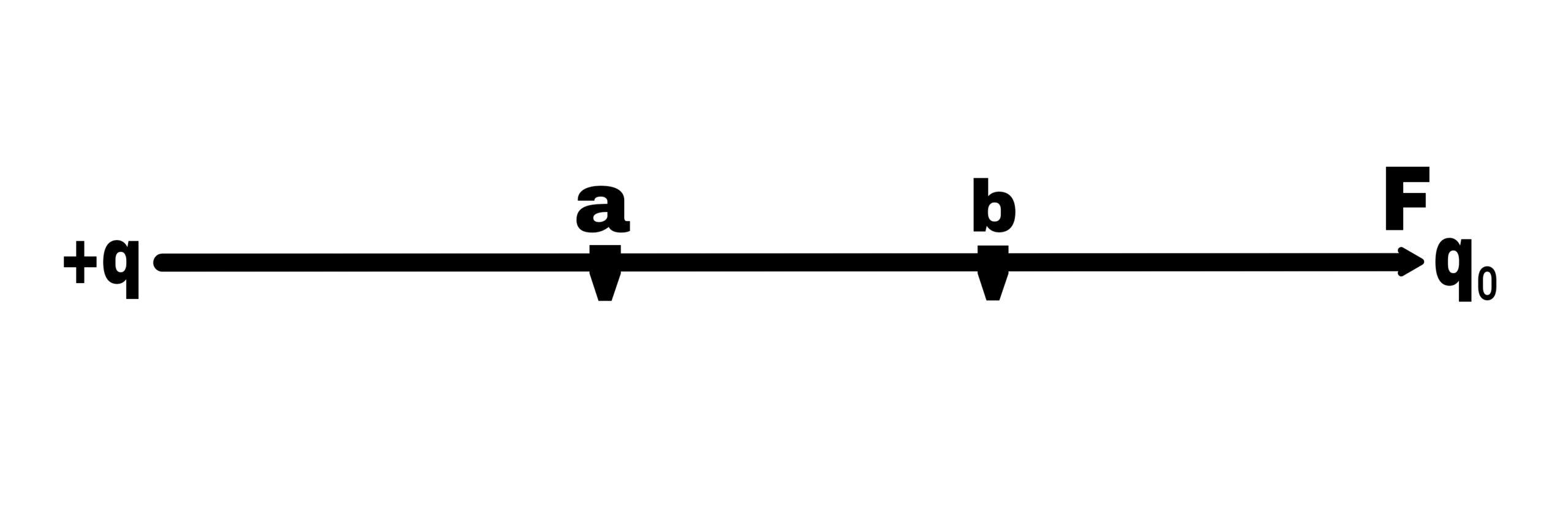
The work done in moving a charge b/w two points in an electric field
Electric potential difference b/w the point a and point b
Va – Vb = W/q₀
W = (Va – Vb)q₀
Where W is work done in the moving a positive test charge from one point to the another
W = ∆V.q₀ _______ (1)
If a charged particle is free to move in an electric field, then the kinetic energy gained by the charge in moving from one point to another is equal to the work done.
So,
Kinetic energy = Work done
If the mass of the charged particle is m and velocity is V,
Then,
Kinetic energy = ½.mV²
½.mV² = q₀.∆V
V = √(2.q₀.∆V)/m
Where,
V is velocity of the charged particle.
The e- (electron) volt is a very small unit of energy.
One e- (electron) volt (1e.v) is the energy
which,
W = ∆V.q₀
W = q₀(Va – Vb)
If
q₀ = 1.e
(Va – Vb)=∆V=1V
W= 1.e.v
1.e.v = 1e.1v
1.e.v = 1.6×10⁻¹⁹×1
1.e.v = 1.6×10⁻¹⁹ joule