Electric potential due to electric dipole
1. Electric potential at a point in axial position of electric dipole
Suppose we want to calculate the electric potential at a point P situated at a distance r from the centre O of an electric dipole having dipole moment P
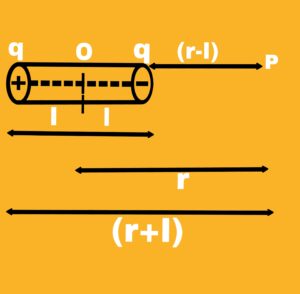
Electric potential at point P due to +q charge
V₁ = [1/4π∈₀][q/r-l]
Similarly,
Electric potential at point P due to -q charge
V₂ = [1/4π∈₀][-q/r-l]
Hence, the resultant potential at point P is
V = V₁+V₂
V = [1/4π∈₀][q/r-l] – [1/4π∈₀][-q/r-l]
V = q/4π∈₀[1/(r-l) – 1/(r+l) V = q/4π∈₀[r+l-r+l]
V = q/4π∈₀[2l(r²-l²)]
V = 1/4π∈₀[2l.q(r²-l²)]
V = 1/4π∈₀[P/(r²-l²)]
Since,
l<<r
V = [1/4π∈₀].P/r²
If the dipole is placed in a medium whose dielectric constant is K, then the resultant potential
V = [1/4π∈₀K].q/r²
2. Electricity located on the neutral line of the electric dipole Potential
Suppose there is an electric dipole with dipole moment P. We have to calculate the electric potential at a point P situated at a distance r from the centre O in the neutral position.
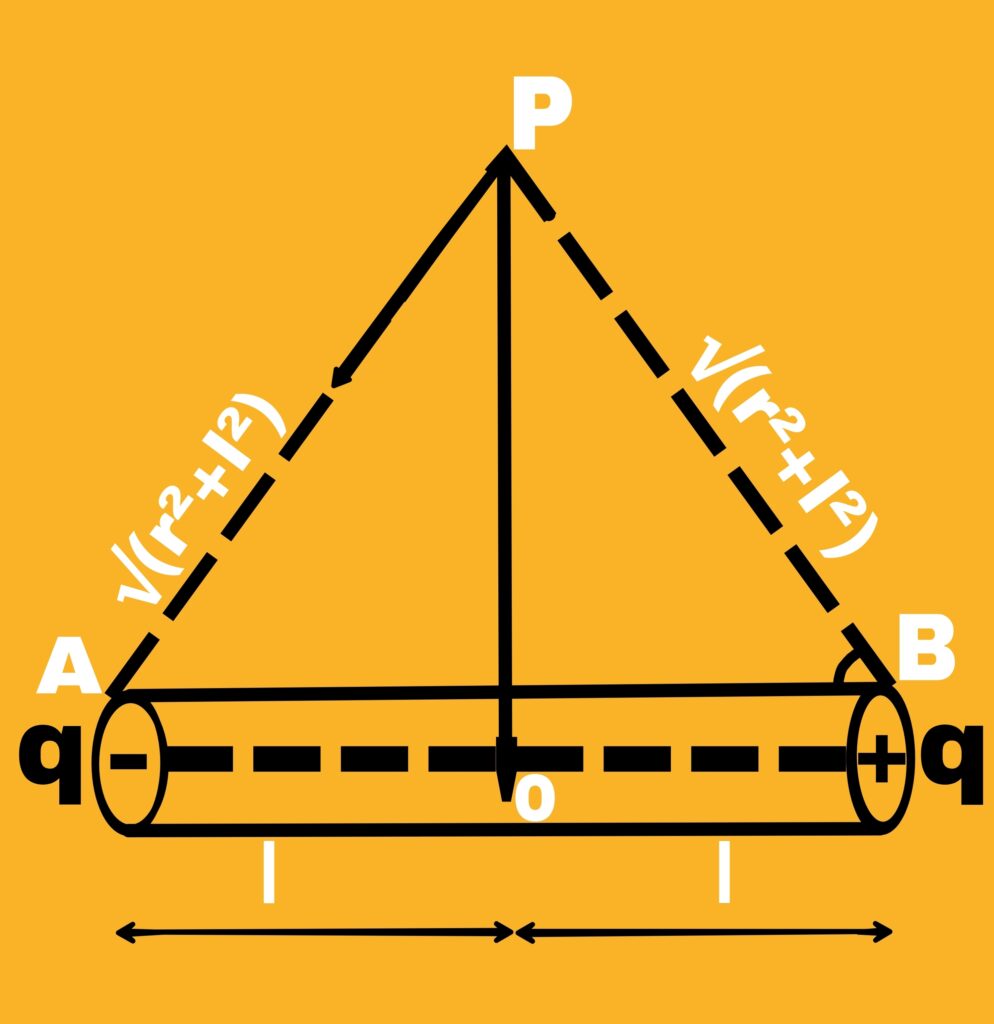
Electric potential at point P due to +q charge
V₁ = [1/4π∈₀][q/√(r²-l²)]
Similarly,
Electric potential at point P due to -q charge
V₂ = [1/4π∈₀][-q/√(r²-l²)]
Hence, the resultant potential at point P is
V = V₁+V₂
V = 0
3. Electric potential due to group of point charges
Electric potential due to several charges at a point can be known by adding them algebraically. If a point has +q₁, +q₂, -q₃ and If the point charges of -q₄ are at a distance of r₁, r₂, r₃ and r₄ respectively, then the total potential at that point
V = [1/4π∈₀][+q₁/r₁] + [1/4π∈₀][+q₂/r₂] + [1/4π∈₀][-q₃/r₃] + [1/4π∈₀][-q₄/r₄]
V = 1/4π∈₀[(q₁/r₁)+(q₂/r₂)-(q₃/r₃)-(q₄/r₄) volt