What is magnetic field class 12th

Magnetic field

The field around a magnet in which a magnetic needle is subjected to a torque, causing it to rotate and stay in a fixed direction.

The direction of a line drawn from the south pole to the north pole of a small magnetic needle suspended freely at any point in the field is called the direction of the magnetic field.

Magnetic Field Due to a Serial Conductor (Biot-Savart’s Law)

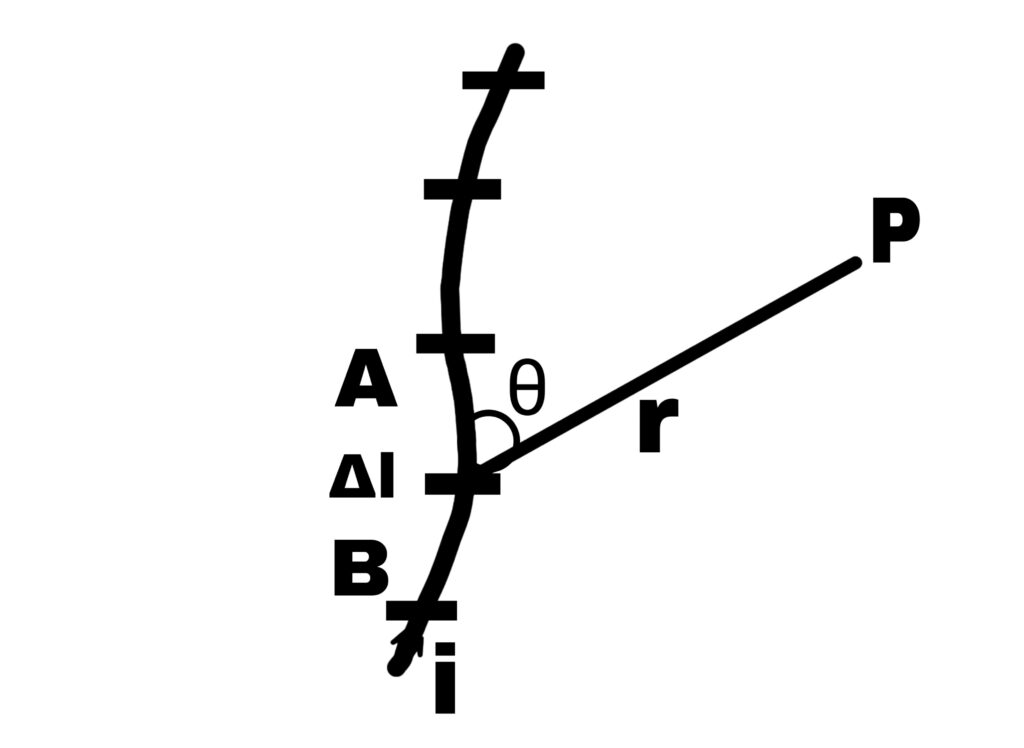
When current flows through a conducting wire, a magnetic field is generated around it, which was first calculated by Biot-Savart.

To determine the magnetic field produced by a serial conductor, Biot-Savart first divided the serial conductor into equal small parts.

Let another small part AB be of length ∆l. The magnetic field at point P is calculated using this small part.

The magnetic field AB produced by the small part ∆l depends on the following factors.

1. It is directly proportional to the electric current i flowing through the conductor.

That is, ∆B ∝ i

2. Is directly proportional to the length ∆l of that conductor element.

That is, ∆B ∝ ∆l

3. The magnetic field produced is directly proportional to the sine of the angle θ formed between the length of the element and the line joining the element to point P.

That is, ∆B ∝ Sinθ

4. Is inversely proportional to the square of the distance r from point P.

That is, ∆B ∝ 1/r²

Combining the above four rules gives,

∆B ∝ i.∆l.Sinθ/r²

∆B = (μ₀/4π)(i.∆l.Sinθ/r²)

Where,

(μ₀/4π) is a constant and its value is 10⁻⁷ N/A².

μ₀ is called the magnetization of vacuum and its value is 4π × 10⁻⁷ N/A².

Dimension of μ₀

μ₀ = [MLT⁻²]/[A²]

μ₀ = [MLT⁻²A⁻²]

Relation between vacuum magnetism μ₀ and vacuum permittivity ε₀

μ₀/4π = 10⁻⁷ N/A² —- (1)

1/4πε₀ = 9×10⁹ N.m²/c² —- (2)

Equation (1/2),

μ₀.ε₀ = 1/(9×10¹⁶)

√μ₀.ε₀ = 1/(3×10⁸)

1/√μ₀.ε₀ = 3×10⁸ m/sec

Magnetic field due to a rectilinear serial conductor of finite length

Suppose a rectilinear serial conductor CD is carrying a current i. We want to calculate the magnetic field at a point P near the conductor.

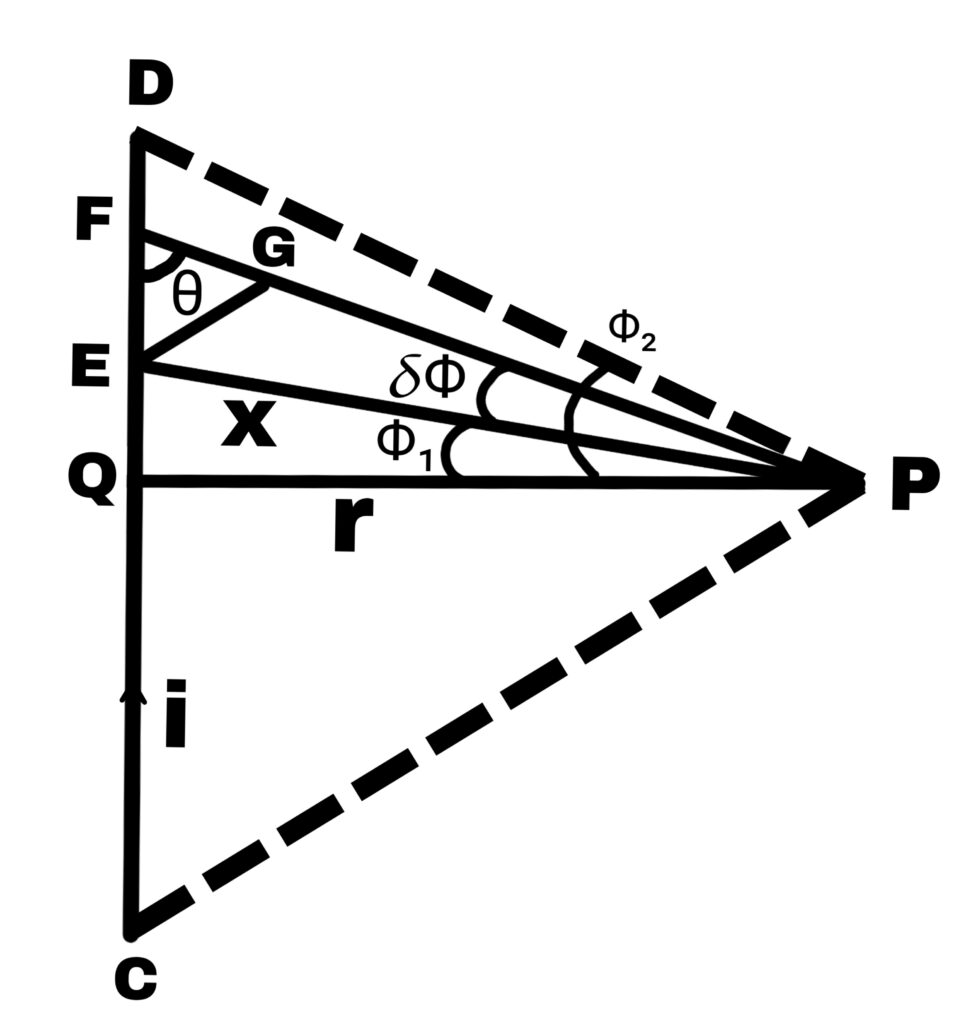
To find the magnetic field intensity at point P, divide the rectilinear conductor CD into small, equal parts.

The finite conductor has a small component EF, which has a length δl and a distance x from point P.

Therefore,

The magnetic field at point P due to this element is given by

δB = (μ₀/4π).(i.δl.Sinθ)/x²

From ∆EFG,

EG = δl.Sinθ

OR,

x.δΦ = δl.Sinθ

δB = (μ₀/4π).(i.x.δl)/x²

δB = (μ₀/4π).(i.δΦ)/x

In ∆QPE,

CosΦ = r/x

x = r/CosΦ

Since,

δB = (μ₀/4π).(i.δΦ)/(r/CosΦ)

δB = (μ₀/4π).(i.CosΦ.δΦ)/r

Or, the magnetic field at point P due to the entire conductor Magnetic field at P

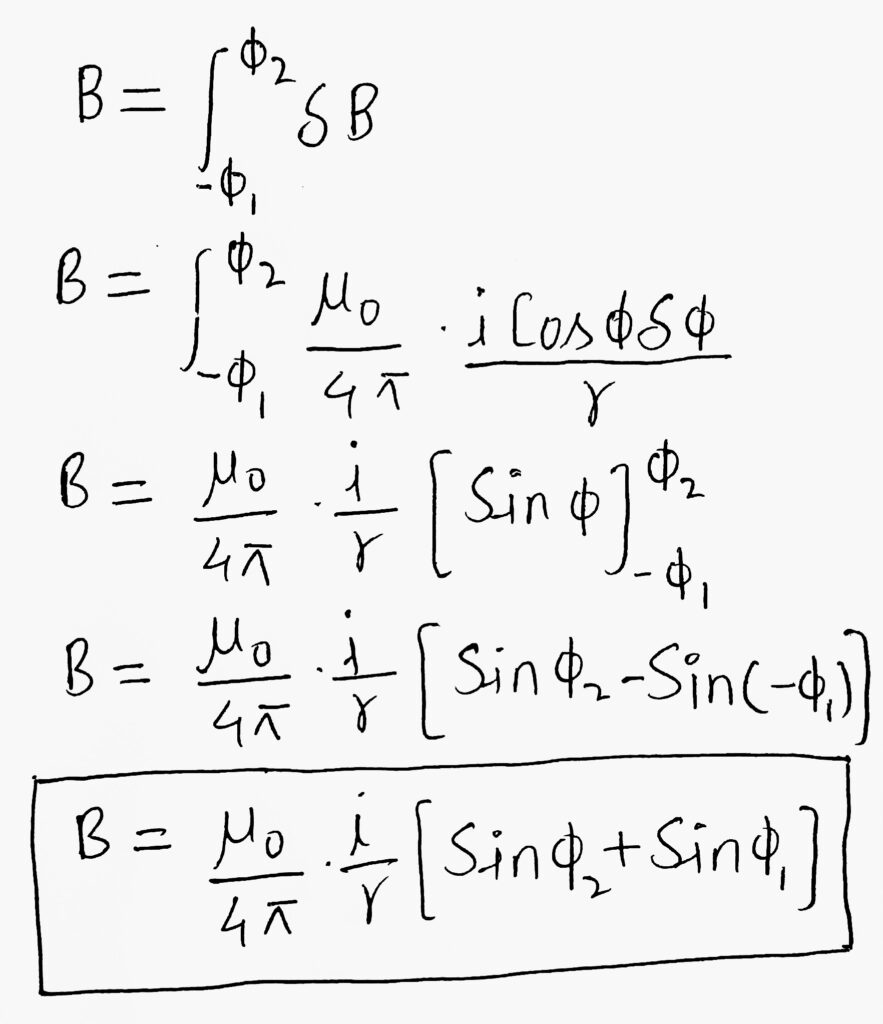
special cases

Case 1–

Φ₁ = Φ₂ = 90

B = (μ₀/4π).i/r[SinΦ₁+SinΦ₂]

B = (μ₀/4π).i/r(1+1)

B = (μ₀/2π).i/r

Case 2-

If point P is near the end of the conductor at a distance r from the conductor then Φ₁ = π/2 and Φ₂ = 0.

Therefore,

The intensity of the magnetic field in this situation

B = (μ₀/4π).i/r[Sine90+Sin0]

B = ( μ₀/4π)i/r

Ampere’s circuit Rule

Statement-

The linear integral of the magnetic field B along the boundary of a closed circuit is μ₀ times the net current i enclosed by the path.

That is,

∮→B→dl = μ₀.i

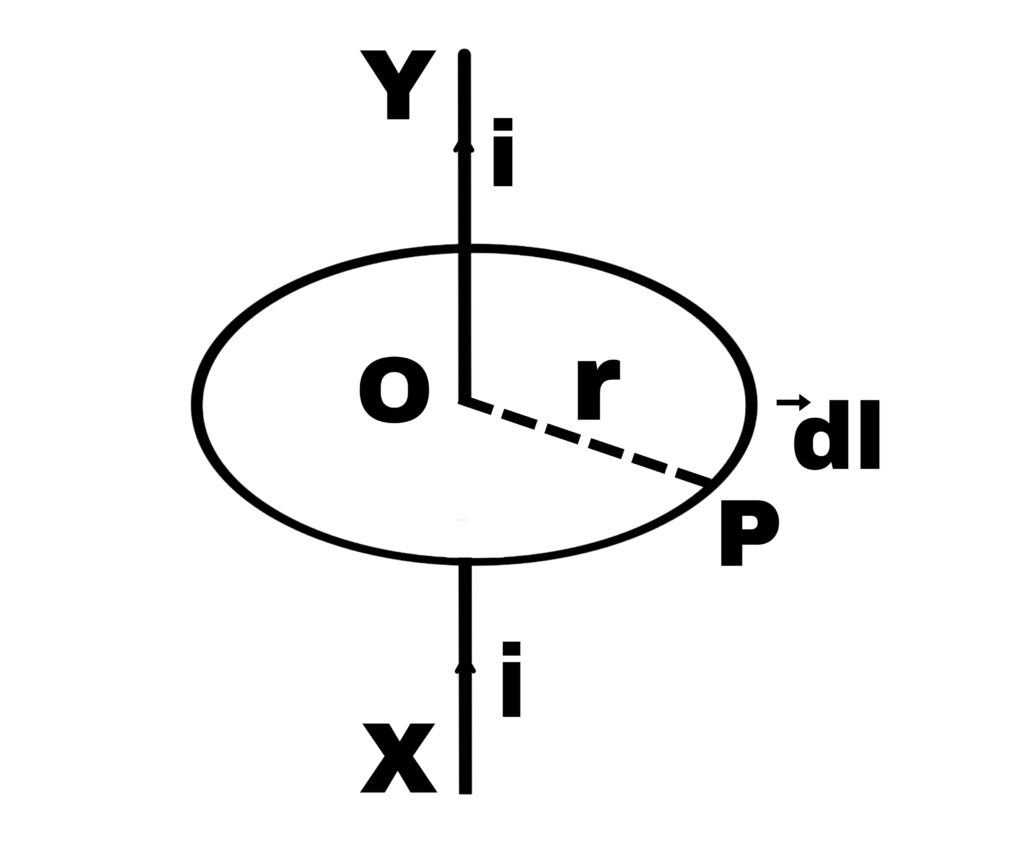
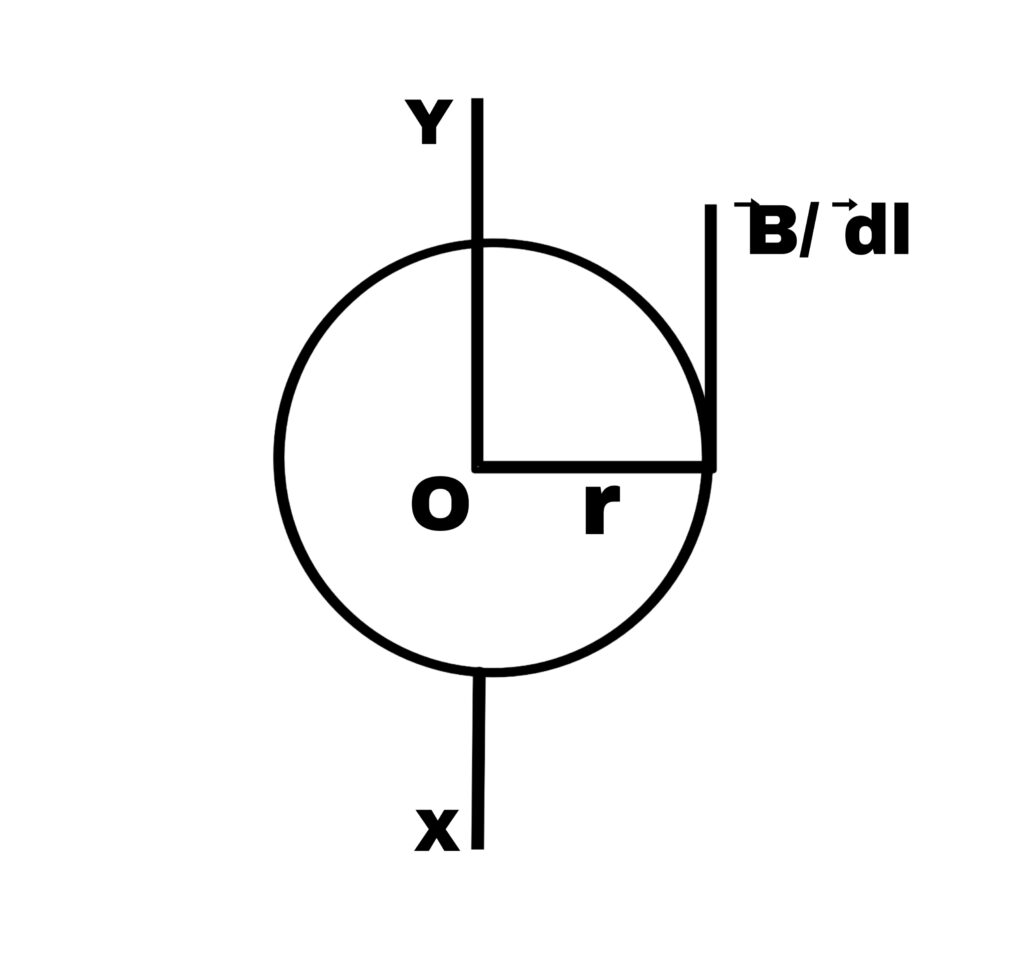
Let xy be a long wire perpendicular to the plane of the paper carrying current i.

Let xy be a circular path of radius r with center o on the wire.

Hence,

The value of the magnetic field at any point P on the circular path is

B = μ₀.i/2πr

Since,

At every point on the circular path,

⃗B and dl are in the same direction.

Therefore,

Linear integral along the magnetic path

∮→B→dl = ∮B.dl.Cos0

∮→B→dl = B∮dl

∮→B→dl = (μ₀i/2πr).2πr

∮→B→dl = μ₀i

Application of Ampere’s Law

Magnetic field due to a straight current-carrying wire of infinite length :-

Magnetic field due to a straight current-carrying wire of infinite length.

Suppose a long wire is carrying current,

i.e., a point P at a distance r from the wire, where the magnetic field intensity is to be determined. To do this, first draw a circle of radius r.

Since the magnetic field value will be the same at every point on the circular path, and B and dl are in the same direction,

∮→B→dl = ∮B.dl.Cos0°

By Ampere’s law,

μ₀i = B.∮dl

μ₀i = B.2πr

B = (μ₀/2π).i/r