Series and parallel circuits

Series circuit

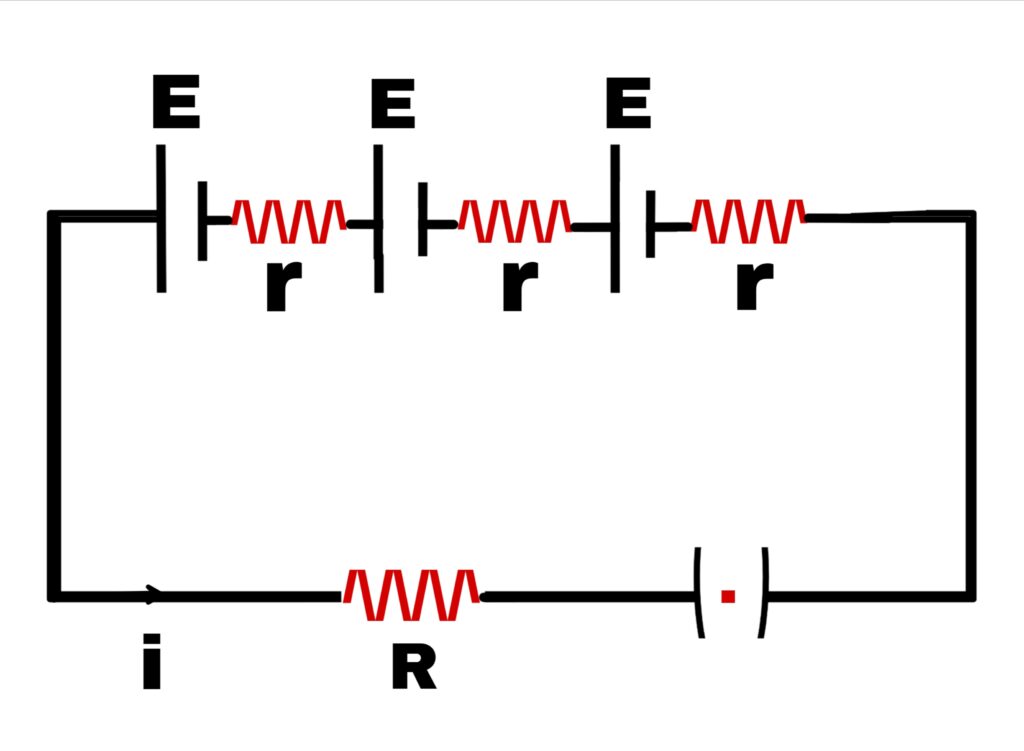
In this type of combination, the negative pole of one cell and the positive pole of the other, the negative pole of the second and the positive pole of the third, the negative pole of the fourth and so on, all the cells are connected.

Suppose n cells are connected in series and the electromotive force of each cell is E and the internal resistance is r. In this case, all the cells are connected to an external R.

So the resultant electromotive force of all the cells = n.E

Total internal resistance = n.r

The total resistance of the circuit = (nr+R)

So the current flowing in the circuit is

i = n.E/(nr+R)

Case 1

If n.r << R, then in this case the current in the circuit is

i = n.E/R

In this case,

When the total internal resistance of the cells is much less than the external resistance, then the current generated by the cells will be n times the current flowing in one cell.

Case 2

If n.r >> R

i = n.E/n.r

i = E/r

In this case, if the total internal resistance of all cells is much more than the external resistance, then the current flowing through n cells will be equal to the current flowing through one cell.

Parallel series

In this type of series, the positive poles of all cells are connected to one point and the negative poles to the other point.

Suppose n cells are connected in normal series, each of which has an electromotive force E and internal resistance r and the external resistance of this battery of n cells is R. The cells are connected in parallel series.

So the electromotive force of the entire battery will be E. If the internal resistance of all the cells is R₁, then

1/R₁ = 1/r + 1/r +——– upto n terms

1/R₁ = n/r

R₁ = r/n

Hence the total resistance of the circuit will be (r/n+R).

Hence the current flowing in the external circuit

i = E/(r/n+R)

i = n.E/(r + n.R)

Case 1

If r <<R

In this case the current flowing in the cell

i = n.E/n.R

i = E/R

That is, the electric current of the total circuit will be equal to the electric current obtained from one cell.

Thus there will be no benefit in connecting cells of low internal resistance in parallel.

Case 2

If r>>R

That is,

If the internal resistance of the cells is very large compared to the external resistance, then the current in the circuit

i = n.E/r

Therefore,

When the internal resistance of the cells is very large compared to the external resistance, then they should be connected in parallel.

Case 3

If the electromotive force and internal resistance of the cells connected in parallel are different, then the value of the current obtained in any external circuit from these cells is found from Kirchhoff’s law.

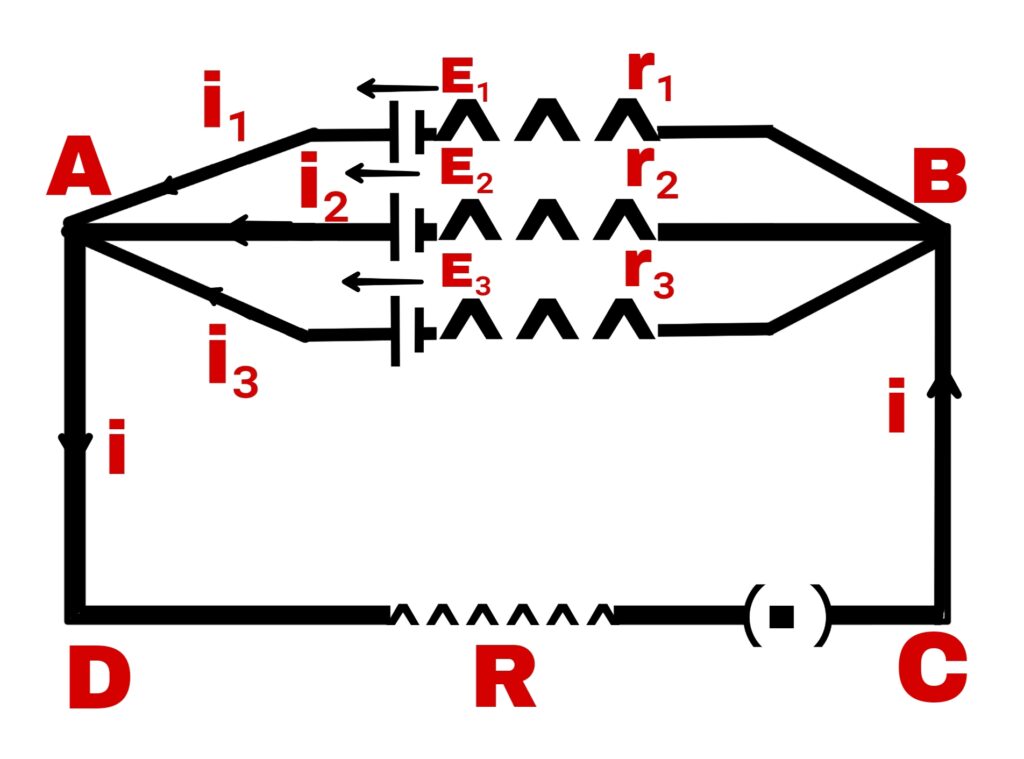
Suppose three cells are connected in parallel whose electromotive force is E₁, E₂ and E₃ and internal resistance is r₁, r₂ and r₃ respectively. If the current generated by these cells is i₁, i₂ and i₃ respectively, then

From K.C.L

i = i₁ + i₂ + i₃ ———-(1)

From K.V.L

For closed pass ADCBE₁A

i.R + i₁r₁ = E₁

i₁ = (E₁- iR)/r₁

For closed pass ADCBE₂A

i₂.r₂ +iR = E₂

i₂ = (E₂- iR)/r₂

Similarly, for closed pass ADCBE₃A

i₃ = (E₃- iR)/r₃

Putting the values of i₁, i₂, and i₃ in equation (1)

i = (E₁- iR)/r₁ + (E₂- iR)/r₂ + (E₃- iR)/r₃

i = E₁/r₁ + E₂/r₂ + E₃/r₃ -iR[ 1/r₁+1/r₂+1/r₃ ]

i + iR[1/r₁+1/r₂+1/r₃ ] = E₁/r₁ + E₂/r₂ + E₃/r₃

i[1+R(1/r₁+1/r₂+1/r₃)] = E₁/r₁ + E₂/r₂ + E₃/r₃

i = [E₁/r₁ + E₂/r₂ + E₃/r₃]/[1+R(1/r₁+1/r₂+1/r₃)]

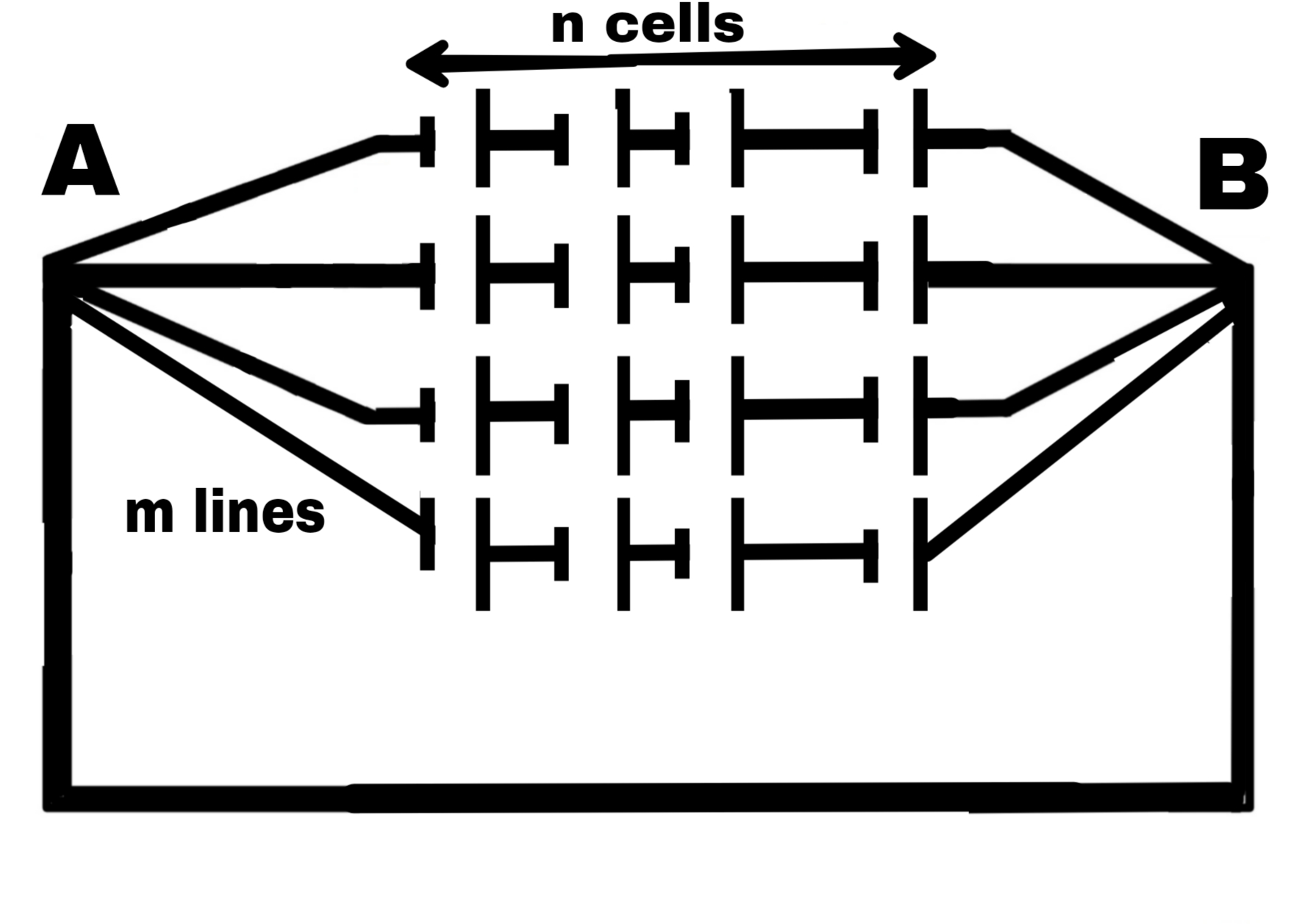
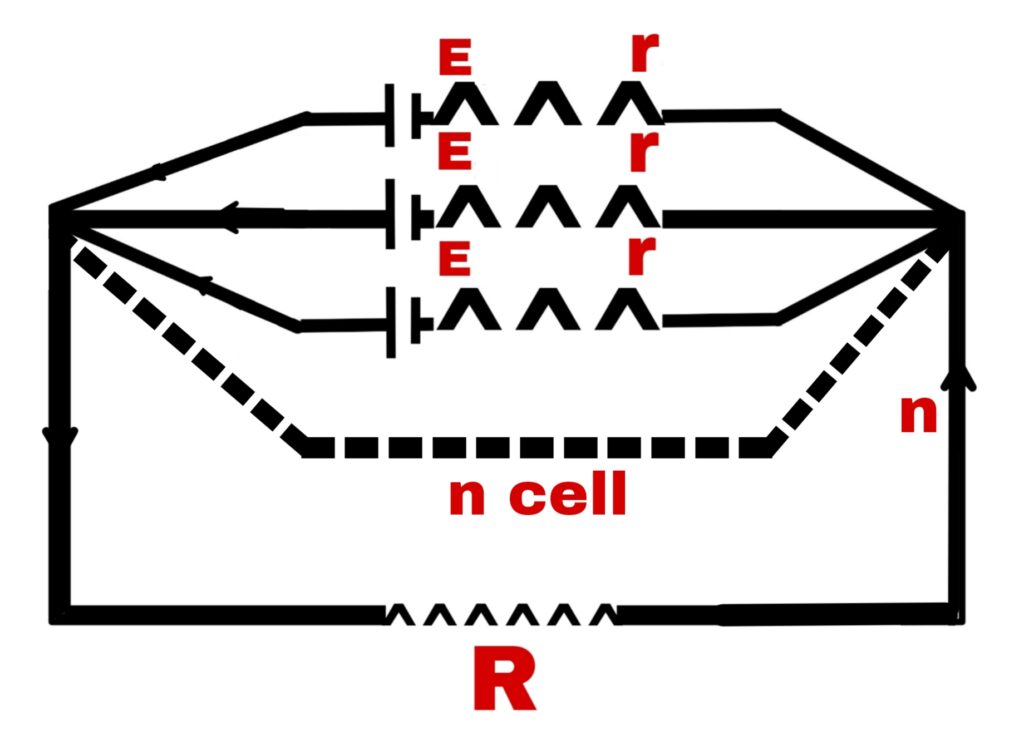
Mixed order circuit or combination circuit

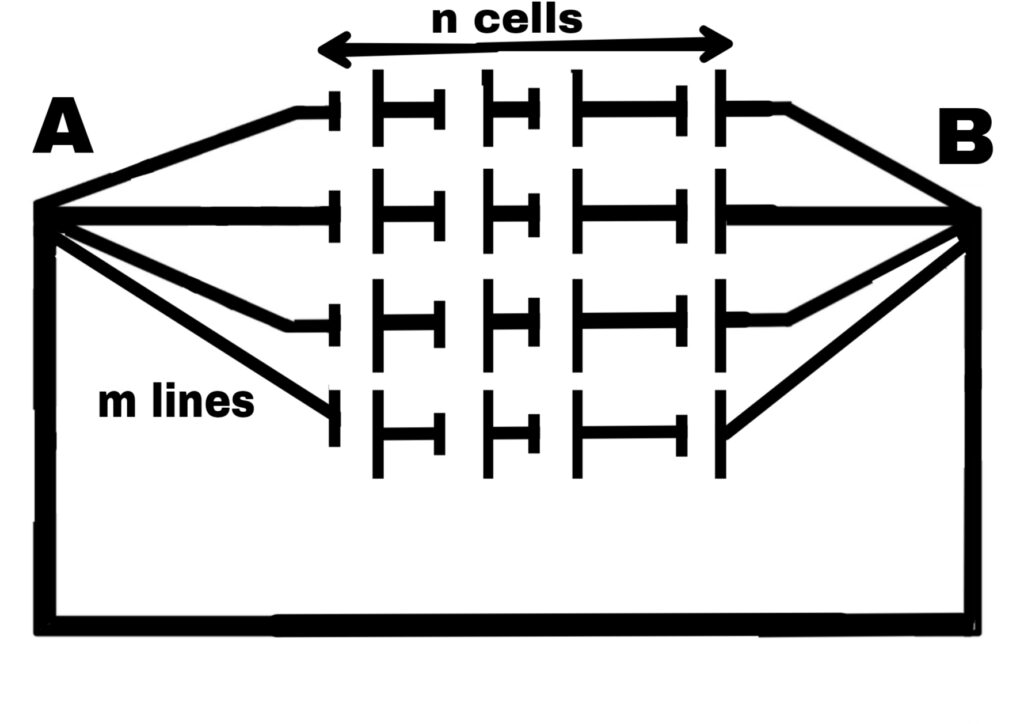
In this type of order some cells are connected in series and all such series are connected in parallel.

Suppose n cells are connected in each row of the series.

Hence, the electric carrier of n cells = n.E

All the series are connected in parallel.

Hence, the electromotive force of the whole battery = n.E

Similarly, the total internal resistance of n cells in a series = n.r

Hence, the total internal resistance of the whole battery

1/R₁ = 1/nr + 1/nr + 1/nr +——— up to m terms

1/R₁ = m/nr

R₁ = nr/m

Hence, the total resistance of the circuit

= (nr/m + R)

Hence, the current flowing in the external circuit

i = n.E/(nr/m + R)

i = m.n.E/n.r + mR

For the value of i to be maximum, the value of (n.r + mR) should be minimum.

n.r + mR = [(√n.r)-(√m.R)]² + 2√m.n.r.R

For n.r + mR to be minimum, the value of [(√n.r)-(√m.R)]² should be minimum.

When

[(√n.r)-(√m.R)]² = 0

Or,

√n.r – √m.R = 0

√n.r = √m.Rn.

r = m.R

R = n.r/m

But (n.r/m) is the total internal resistance of the battery.

Hence,

In mixed order, the value of current in the external circuit will be maximum when the total internal resistance of the battery is equal to the external resistance.

Hence,

The maximum current flowing in the external circuit is

i max. = n.E/(nr/m + R)

i max. = n.E/R+R

i max. = n.E/2R