Electrical current and Ohm’s Law

Electric current 

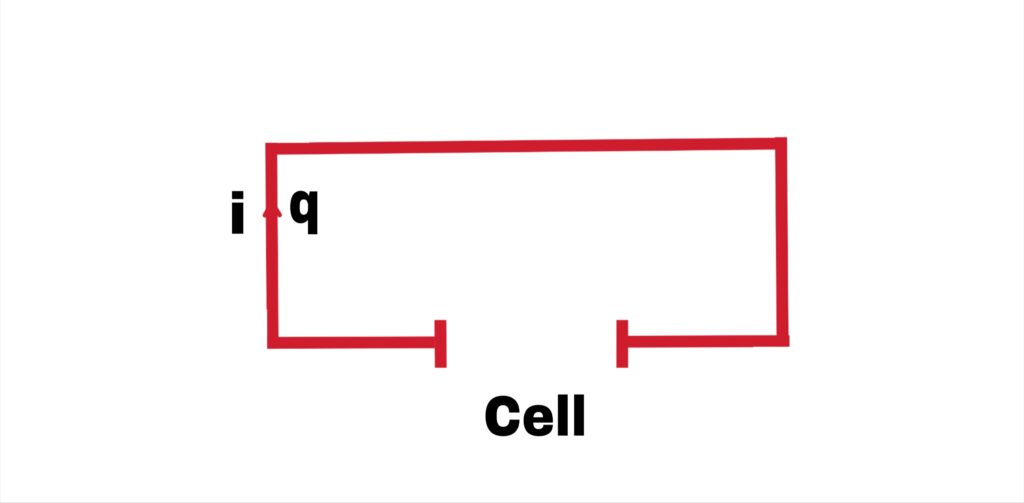
If q charge flows in a circuit in time t, then electric current flowing in circuit is__

i = q/t Ampere

When,

t = 1 sec

i = q Ampere

Therefore,

The total charge flowing in a circuit in one second is called electric current. Electric current is a scalar quantity.

Current density

It is represented by j.

If a current of i ampere is uniformly distributed in an area A of a conductor in a circuit, then the current density is__

j = i/A

When,

A = 1 m²

j = i

Therefore,

The electric current flowing in a unit area of a conductor is called the current density. It is a vector quantity. 

Relation b/w the velocity of movement of free electrons and electric current

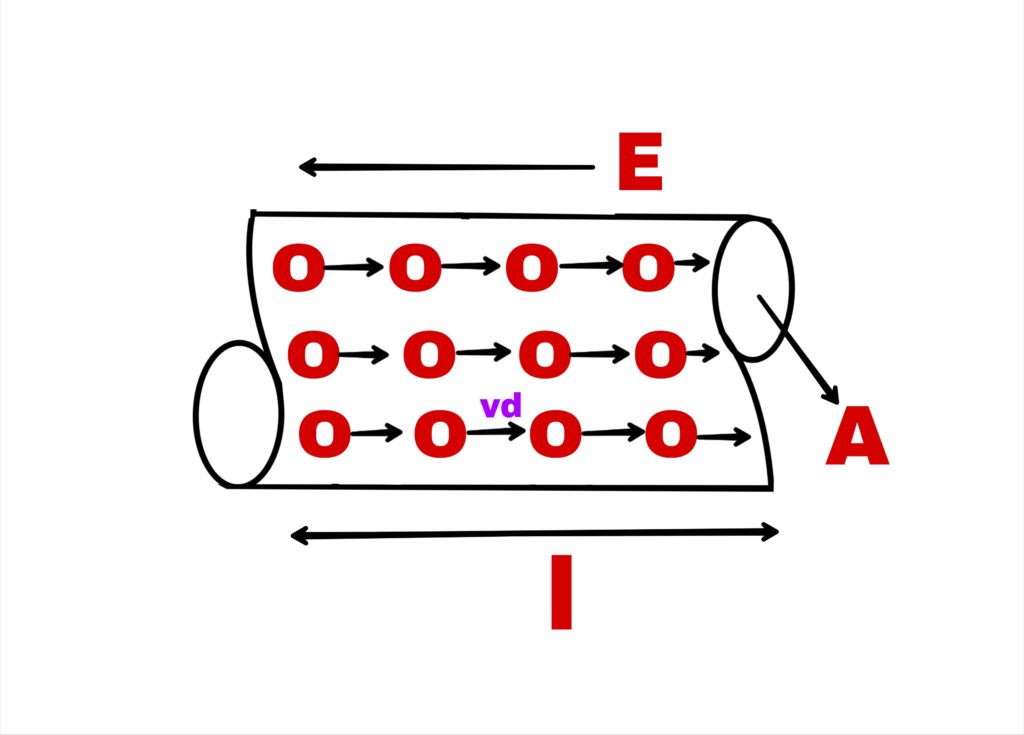
Suppose,

A conductor whose length is l and the area of cross section is A. When a conductor is connected to the battery, an electric field is established in a conductor and the free electrons of the conductor start moving in the opposite direction of the electric field with velocity vd. If the total charge passing through a cross section of a conductor in t seconds is q, then the current flowing through the conductor

i = q/t

If the no. of free electrons in a unit volume is n, then the no. of electrons passing through the cross-sectional area of the conductor in 1 second is__

n.A.vd

If the charge on one electron is e, then the charge passing through cross section of a conductor in t seconds is__

q = (n.A.vd.t)

q/t = (n.A.vd.t).e

q/t = i

i= n.e.A.vd

( if there is a relation b/w drift velocity and electric current. )

Current density Relation between drift velocity

Since current density

j = i/A

j = n.e.A.vd/A

j = n.e.vd

Mobility

The mobility of a charge carrier is the ratio of the magnitude of drift velocity and the intensity of the electric field.

µ = vd/E

If,

E = 1N/C

µ = vd

Velocity of the movement of charge carrier in unit electric field is called mobility of charge carrier.

Unit of µ

µ = vd

µ = meter²/volt-sec

Note

Mobility is always a positive quantity and it depends upon the nature of charge carriers.

For metal electrons,

µₑ = vd/E = e^τ/mₑ

Where

τ = fatigue time of electron

Similarly,

For electrons,

µₕ = eτₕ/mₕ

Where,

mₕ = mass of electron

τₕ = fatigue time of electron

The current density due to e⁻ in terms of mobility is

Jₑ = -nₑ.evd

Jₑ = -nₑ.e(-µₑ.E)

(vd = -µₑ.E)

Jₑ = nₑ.e.µₑ.E

Where

nₑ = number of electrons per unit volume

Current density due to cations,

Jₕ = nₕ.e.vd

Jₕ = nₕ.e.µₕ.E (vd = -µₕ.E)

Where

nₕ = number of cations per unit volume

Hence,

Current density in semiconductor

J = Jₑ+Jₕ

J = nₑ.e.µₑ.E + nₕ.e.µₕ.E

J = ( nₑ.µₑ + nₕ.µₕ )e.E

J = e( nₑ.µₑ + nₕ.µₕ )E

Electrical resistance and electrical conductivity

1. Electrical resistance

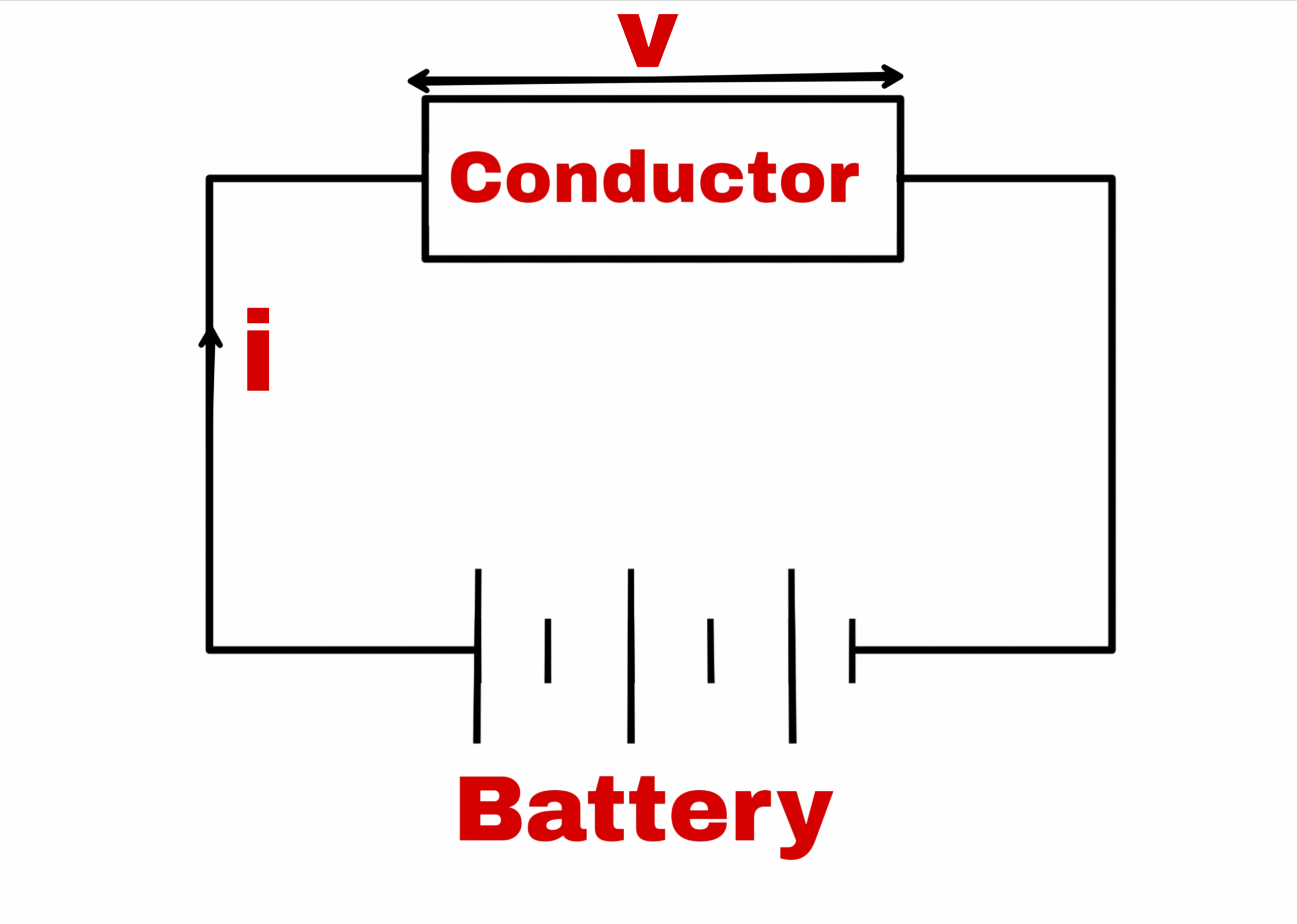
When the ends of a conductor are connected to a battery, the potential difference is established b/w the ends of the conductor, then the electric current flows through the conductor.

Therefore,

Ratio of the electric potential difference and electric current is called electrical resistance of that conductor.

It is represented by R.

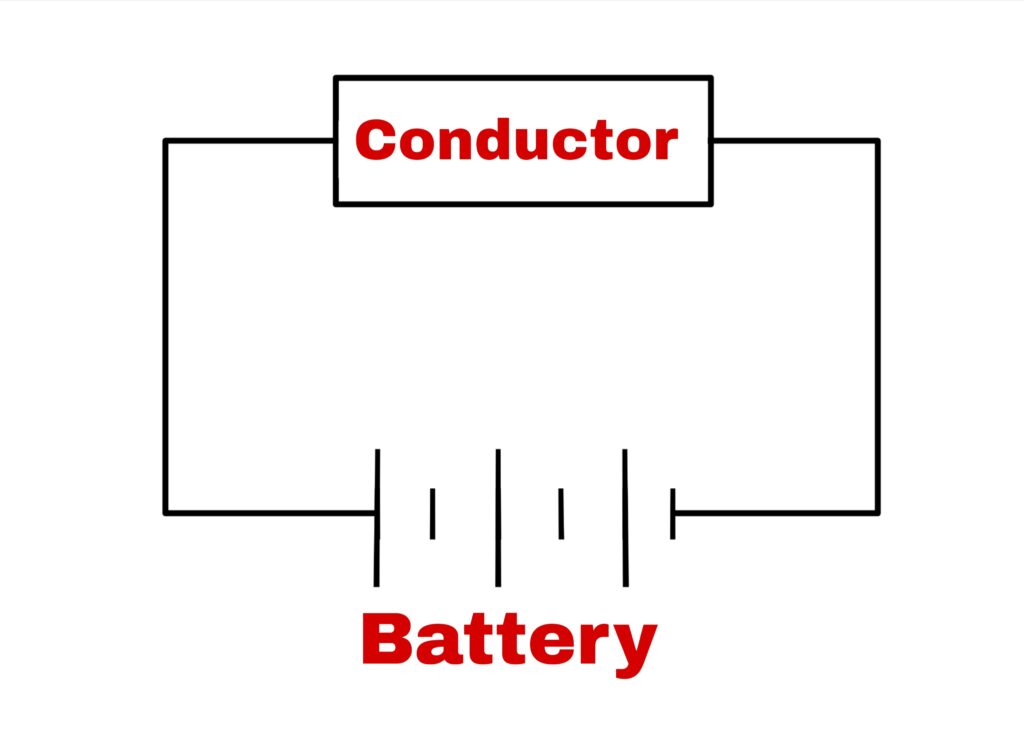
If potential difference b/w the ends of a conductor is V and the current flowing through the conductor is i, then electrical resistance in the conductor is

R = V/i

Unit of R

Ohm

2. Electrical conductivity

The reciprocal of electrical resistance is called electrical conductivity.

Unit

mho or ohm⁻¹

Ohm’s law

According to this law,

If there is no change in the physical state of a conductor, then the ratio of the electric potential difference applied at its ends and the electric current flowing through them is constant.

If electric potential difference applied across the ends of a conductor was V and the current flowing through it was i.

Then,

By Ohm’s law,

V/i = Constant

Ratio of V and i is the resistance.

V/i = R

When a graph is plotted b/w V and i, a straight line is obtained.

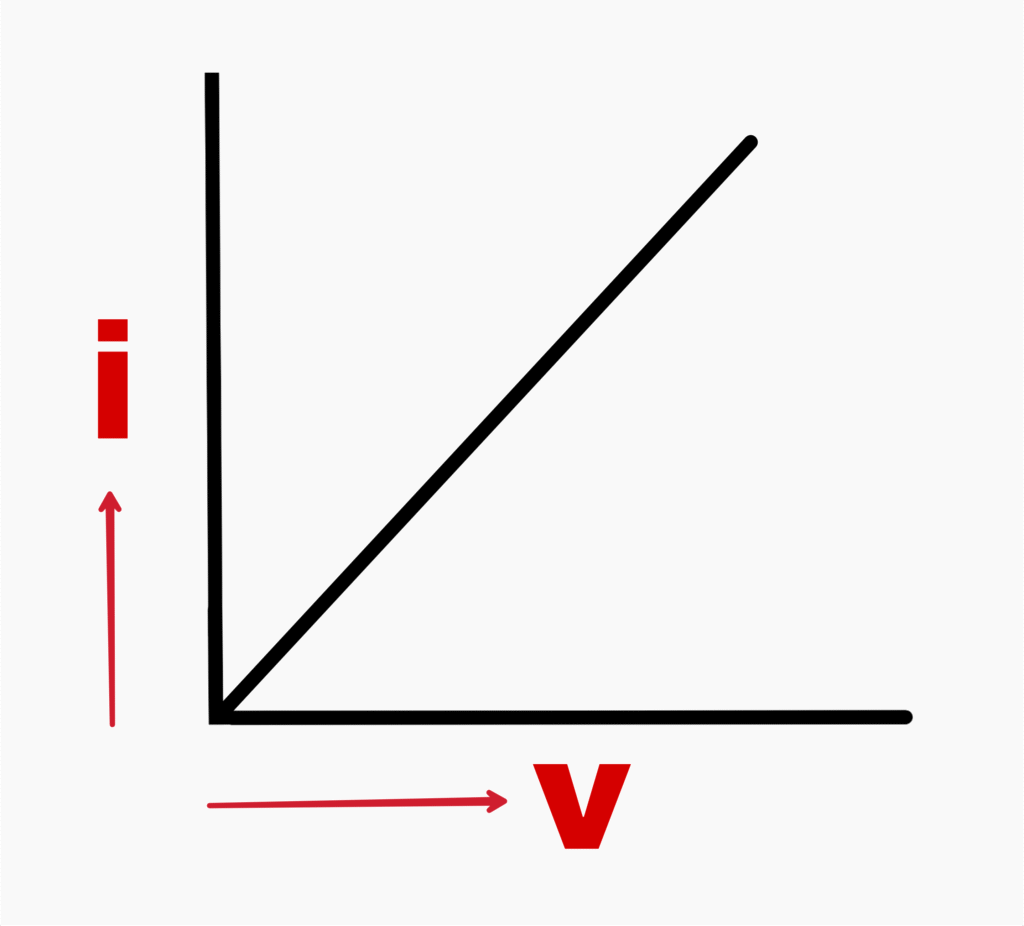
Ohm’s law is true only for conductors. Those substances which do not obey Ohm’s law are called a conductors.

Ohmic and Anohmic Circuits

The circuits which obey Ohm’s law are called Ohmic circuits. For such circuits, the graph drawn b/w V and i is a straight line.

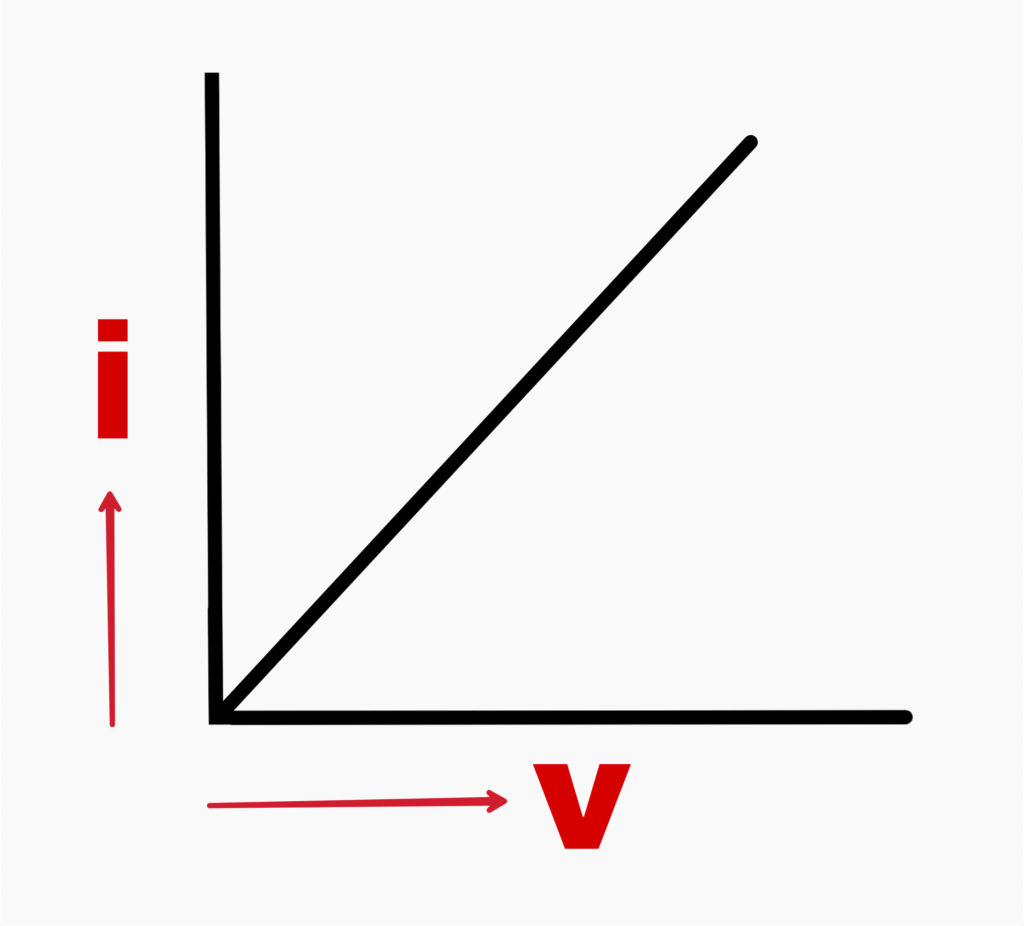
The circuits which do not obey Ohm’s law are called Anohmic circuits. For such circuits, the graph drawn b/w V and i is not a straight line.

That is,

V/i is not constant.

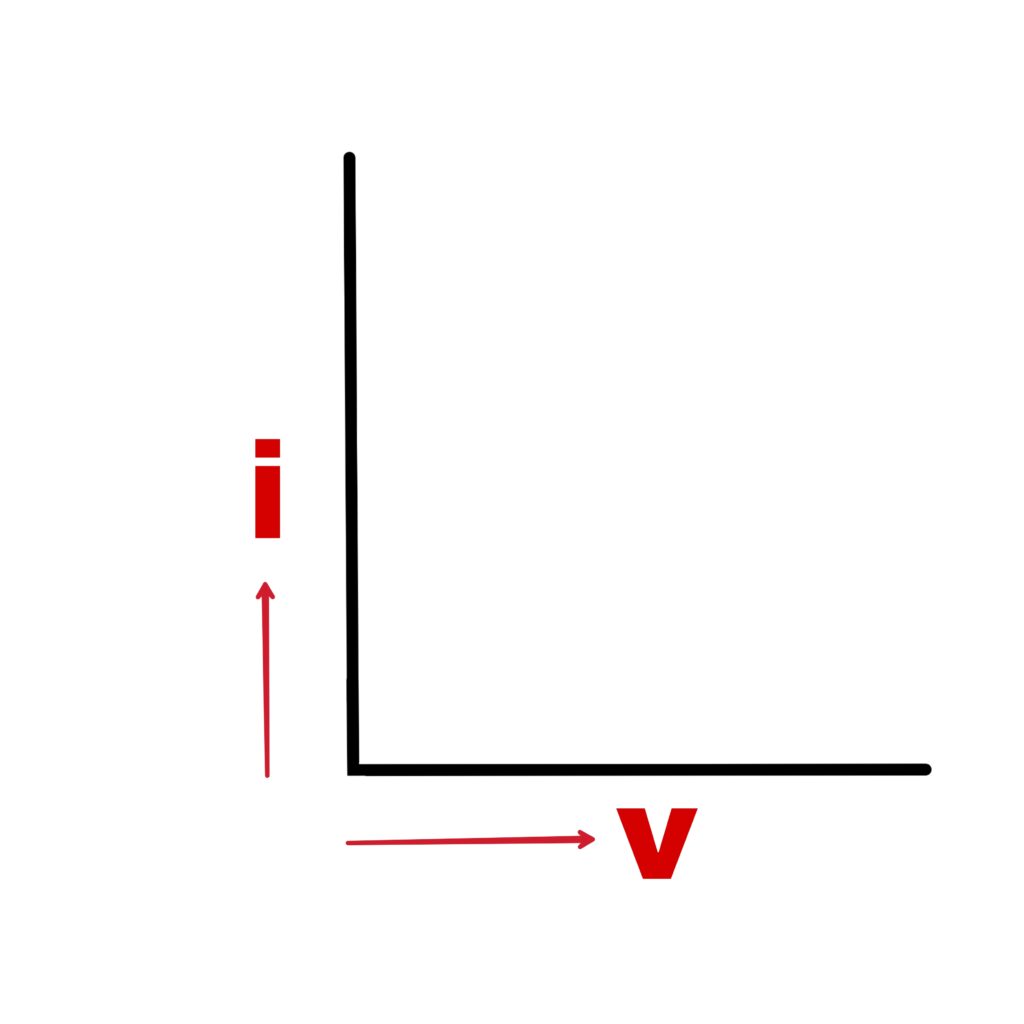
The mixture of metals does not obey Ohm’s law. For such circuits, dynamic resistance is used.

Dynamic resistance

For an ohmic circuit, ratio of the change in potential difference ∆V to the change in current relative to it ∆i is called the dynamic resistance.

Dynamic resistance = ∆V/∆e

Explanation of Ohm’s law on the basis of drift velocity

Suppose the length of metal wire is l and area is A. When a potential difference V is established between its ends, then electric current i starts flowing in it.

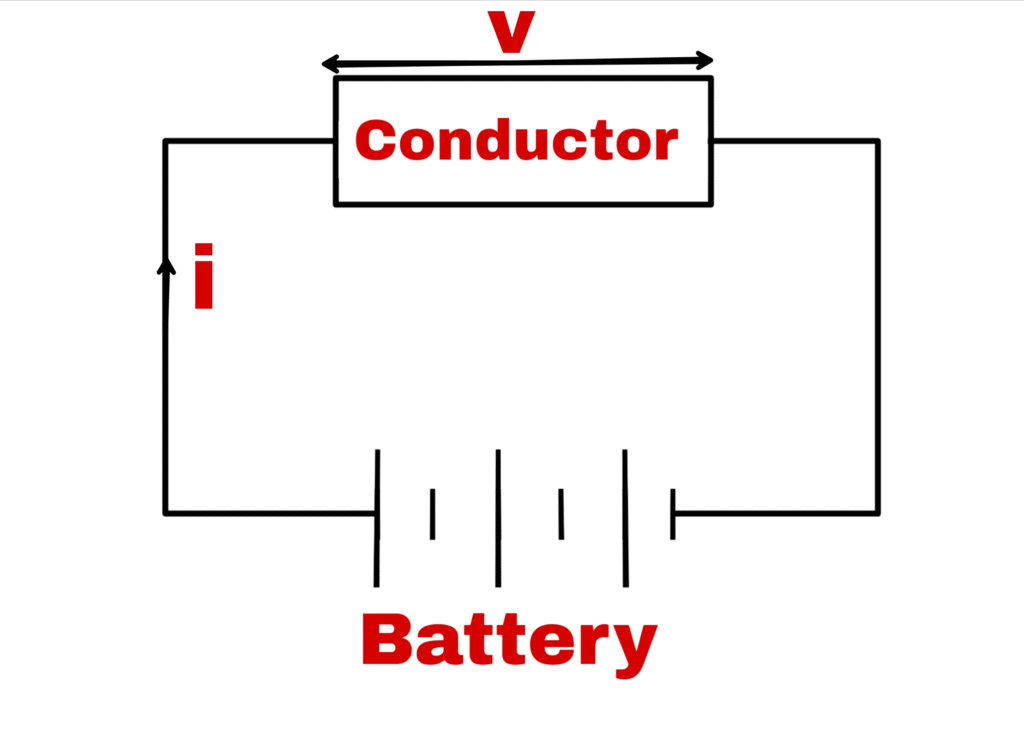
If the number of free electrons in unit volume of the wire is n and drift velocity of the electron is vd.

Then,

i = n.e.A.vd —–(1)

Where e is the charge of electrons.

Since the length of a conductor is l and the potential difference b/w the ends is V.

Hence,

Electric field at each point of the wire

E = V/l

Force exerted on each free electron by this electric field

F = e.E

F = e.V/l

If the mass of the electron is m,

Then the acceleration produced in the electron due to this force is

m.a = e.V/l

a = e.V/m.l —–(2)

Since the main electrons inside the conductor repeatedly collide with the metal cations, if there is a time interval between two successive rotations of an electron with the cations,

T,

Then

The time interval b/w the rotations of the electron = a.τ

If the thermal velocity of an electron is u₁ at any moment in the absence of an electric field, then in the presence of same electric field its velocity will increase to u₁+aτ₁.

Where,

τ₁ = The time interval of two successive collisions of electron.

Similarly, the velocity of other electron is

u₂+aτ₂, u₃+aτ₃———–

Therefore,

Average velocity of all n electrons will be the tracking velocity of electrons.

Vd = ( u₁+aτ₁ )+( u₂+aτ₂ )+(u₃+aτ₃)+—–

Vd = (u₁+u₂+u₃—–uₙ)/n+a(τ₁+τ₂+τ₃—–τₙ)/n

Vd = aτ ——(3)

Where,

τ = (τ₁+τ₂+τ₃—–τₙ)/n is the average time interval between two consecutive collisions of electrons.

Putting the value of a from equation (2) in equation (3).

Vd = (ev/ml).τ

Putting the value of Vd in equation (1)

i = n.e.A.vd

i = n.e.A.(ev/ml).τ

i = (n.e².A.τ/ml).V

i = [(n.e.²τ)/m].[A/l].V

i/V = (n.e.²τ)/m].[A/l]

V/i = m/(n.e.²τ).(l/A)

m/(n.e.²τ).(l/A) is a constant for a given conductor at a certain temperature. It is called the electrical resistance of the conductor.

Hence,

V/i = R Constant

This is Ohm’s law

Specific resistance or resistivity

It is represented by ρ.

When electric current is impressed in conductor, then ratio of current density i in a conductor and intensity of the electric field is called the specific resistance or resistivity of the conductor.

Hence,

ρ = E/j

If the potential difference between the ends of the conductor is v and the current flowing in the conductor is i, then the intensity of electric field

E = v/l

Where,

l = length of the conductor

j = i/A = current density

A = area of the conductor

Hence,

Specific resistance

ρ = E/j

ρ = [v/l]/[i/A]

ρ = [v/i].[l/A]

ρ = R.A/l

Where, R = electrical resistance

Unit

Ohm.meter

Adjustment of resistance

1. Series combination

Suppose,

Three resistances R₁, R₂, and R₃ connected in a series respectively, the resultant resistance is R.

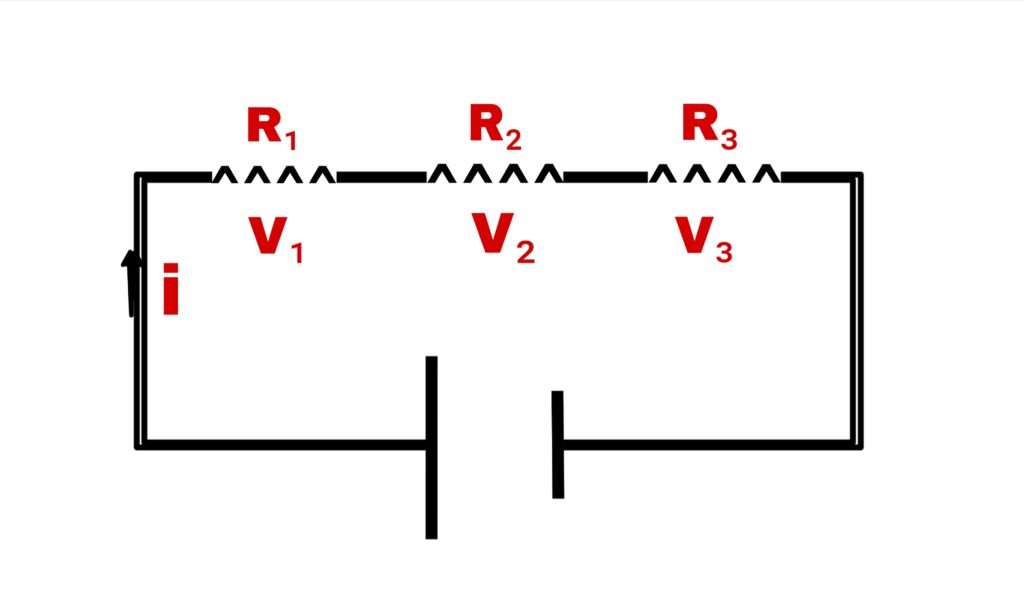
Three resistances connected in series so current through each resistance will be same.

V = V₁+V₂+V₃

iR =iR₁+iR₂+iR₃

R = R₁+R₂+R₃

2. Parallel combination

In this type of combination each resistance has same potential difference.

Suppose three resistances R₁+R₂+R₃ connected in series and their resultant is R.

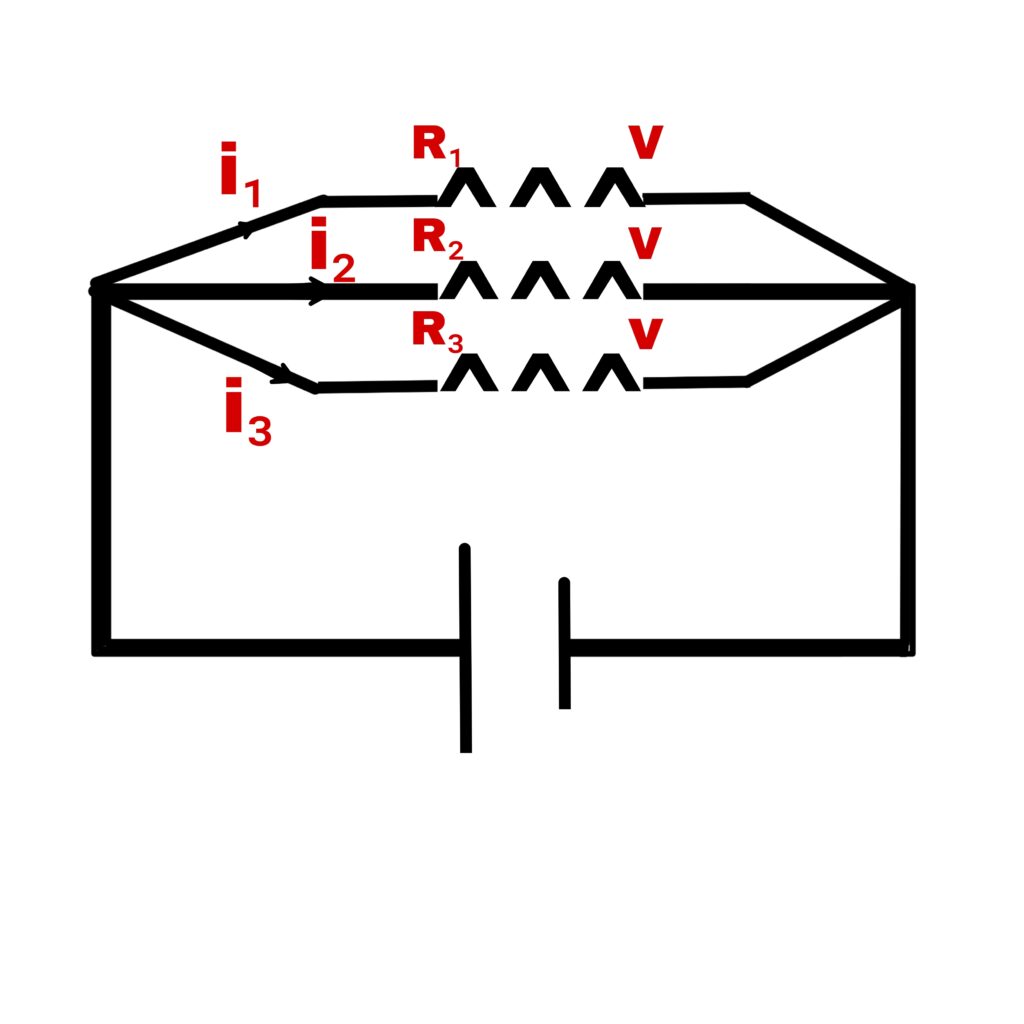
Hence,

Resultant current

i = i₁+i₂+i₃

By Ohm’s law,

V/R = V/R₁+V/R₂+V/R₃

1/R = 1/R₁+1/R₂+1/R₃