What is light
Light is a medium with the help of which we are able to see any objects.
In the absence of light, we cannot see any object because when light falls on an object, it gets reflected and reaches our eyes, then we feel the presence of that object.
Reflection of light
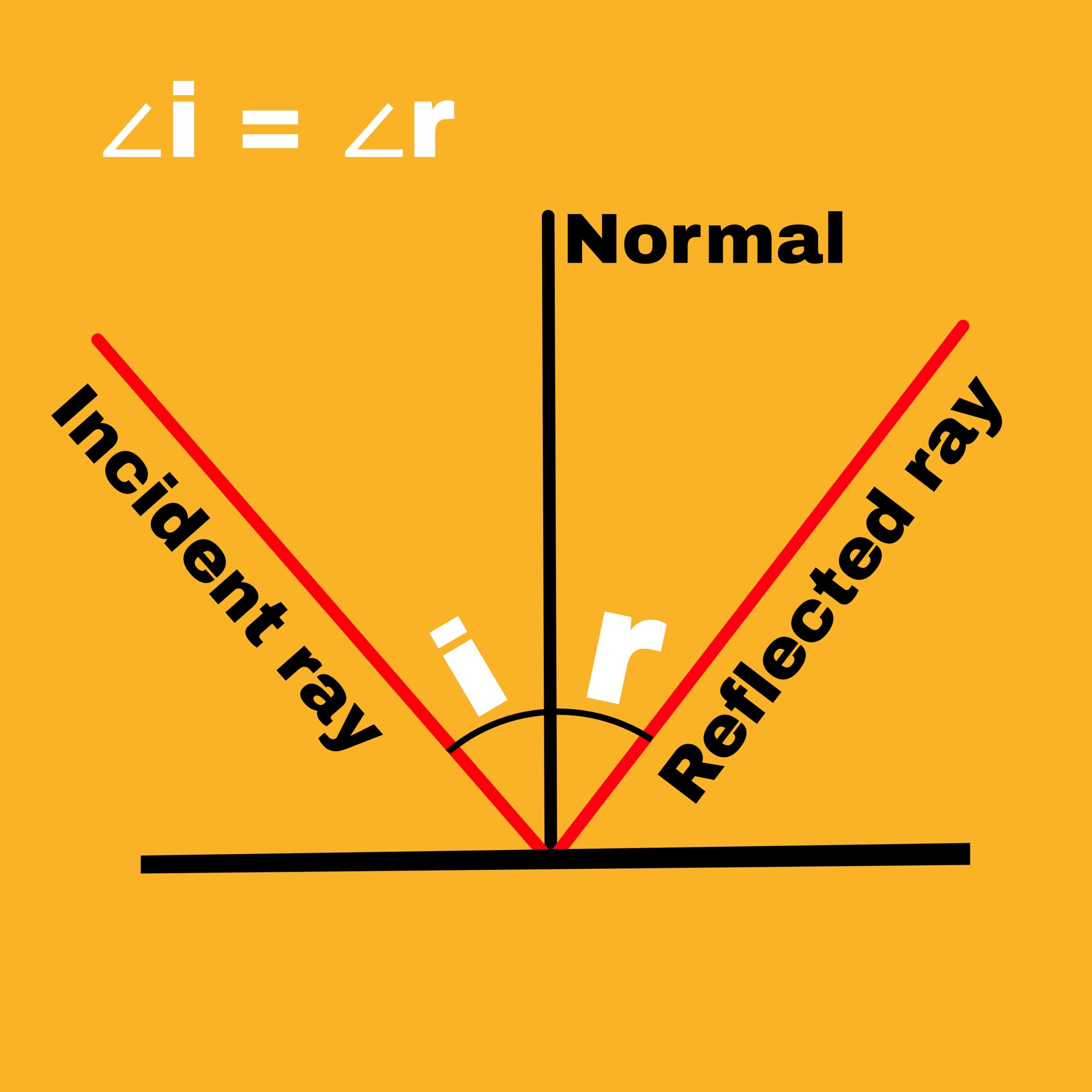
When a traveling ray of light hits a reflective surface, it returns back to the same medium or gets reflected, then this phenomenon is called reflection of light.
Law of reflection
There are two laws of the reflection of light,
1. An angle of incidence is equal to angle of reflection.
2. The incident ray, the reflected ray and the normal drawn at the point of incidence, all three are controlled on the same plane.
Spherical mirror
A mirror whose reflecting surface is spherical is called a mirror.
Concave mirror
A spherical mirror whose reflecting surface is curved inwards is known as concave mirror.

Convex mirror
A spherical mirror whose reflecting surface is curved outwards is known as convex mirror.

Equation/Prove for mirror 1/f = 1/v + 1/u

∠ABC = ∠CB’A’ = 90°
∠BCA = ∠B’CA’
In other words,
∆ABC and ∆A’B’C are similar.
AB/A’B’ = AC/A’C ————– (1)
Similarly,
∆A’B’F and ∆FNM are similar.
MN/A’B’ = FN/A’F ———— (2)
MN = AB
In other words,
AC/A’C = FN/A’F. (From Eq. (1) and (2))
The curved surface is very close to N.
so,
NP = neglected
Therefore,
AC/A’C = FP/A’F
AP-CP/ CP-A’P = FP/(A’P-FP)
-u+r/-r+v = -f/-v+f
(-u+r)(-v+f) = -f(v-r)
uv – uf – rv + rf = -fv + rf
uv = uf + rv – fv
uv = uf + 2fv – fv ( f = r/2, r = 2f )
uv = uf + fv
uv = f ( u + v )
1/f = ( u + v )/uv
1/f = u/uv + v/uv
1/f = 1/v + 1/u Proved
Refraction of light
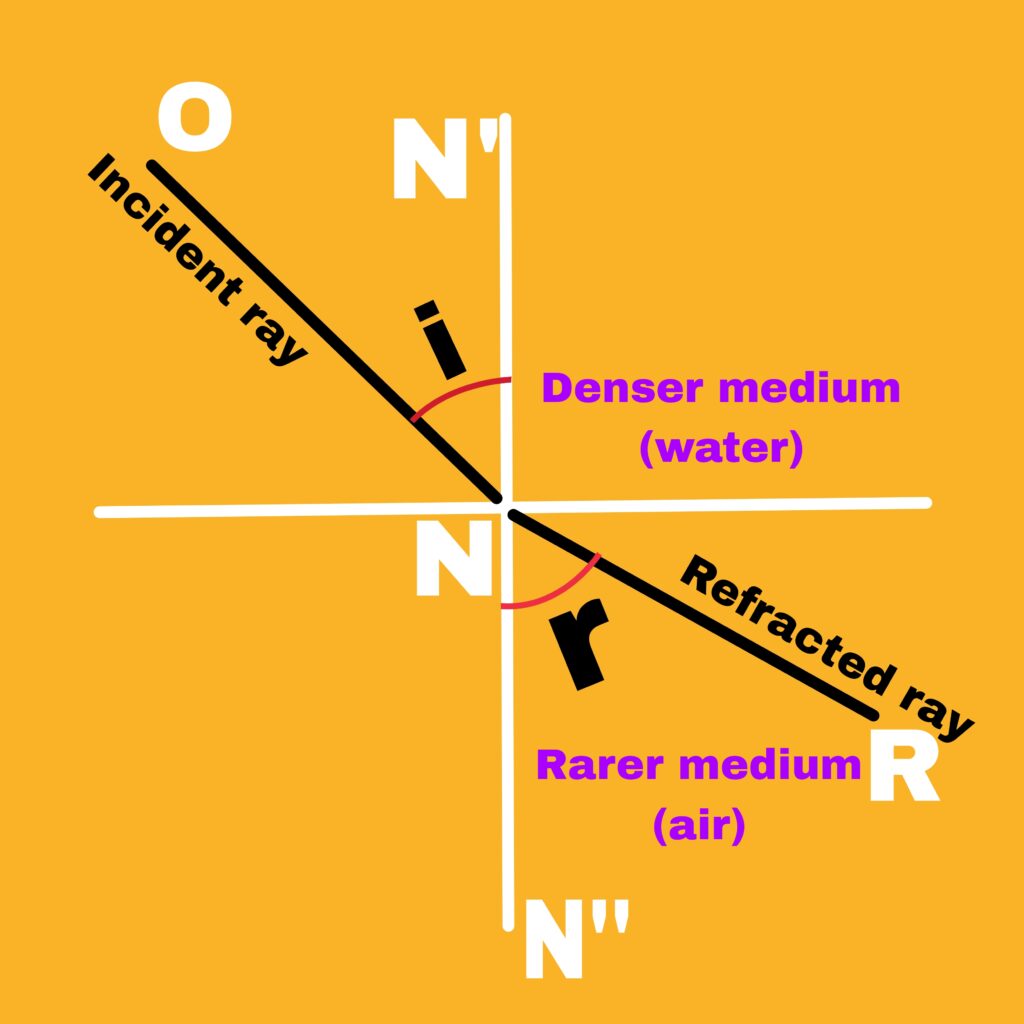
When a ray of light enters from one transparent medium to another transparent medium, it deviates from its straight path, this phenomenon is called refraction of light.
Or,
When a ray of light enters from a rarer medium to a denser medium, it bends towards the normal. Similarly, when a ray of light enters from a denser medium to a rarer medium, it deviates away from the normal, which we call refraction of light. .
(Dense = dense, rarer = less dense)
Law of refraction
This rule is also called Snell’s law.
Snell propounded the following laws of refraction through experiments:
1. The incident ray, the refracted ray and the normal to the refracting surface at the point of incidence, all three lie in the same plane.
2. For any transparent medium pair, the ratio of sine of the angle of incidence and sine of the angle of refraction is a constant.
The angle of incidence (i) and angle of refraction (r) are the angles that the incident ray and the refracted ray make with the normal respectively.
Therefore,
Refractive index of a medium =
Speed of light in vacuum/speed of light in medium
n = sin i / sin r
Where,
n is a constant, which is called the refractive index of the second medium with respect to the first medium.
Refraction of light in a prism
In the prism, the angle of incidence on the first face AB is i and the angle of refraction is r1, while the angle of incidence on the second face AC is r2 and the angle of refraction or exit angle is e.
The angle ∆ between the refracted ray and the incident ray is the angle of deviation
In quadrilateral AQNR,
∠A+∠QNR = 180° __________ (1)
From ∆QNR, ∠r1+∠r2+∠QNR = 180° ________ (2)
From equation (1) and (2) ___
∠A+∠QNR = ∠r1+∠r2+∠QNR
∠A = ∠r1+∠r2 _________ (3)
Since,
r1=r2 = r ______ (4)
Because,
∠i=∠e
Therefore,
A = r+r _____(from Eq.(4))
A = 2r = A/2 ______ (5)
Since,
δ is the sum of deviations on both faces
Therefore,
δ=( i – r1 )+( e – r2 )
δ= i + e – A ________ (6)
Since,
δ= δm (deviation angle)
From equ. (6)
δm = i + i – A _______ ( i = e )
δm = 2i – A
i = ( δm + A ) / 2 _______ (7)
we know that
n = sin i/ sin r
n= sin i [(A+ δm)/2] / sin A/2
{From equations (4) and (7)}
Refraction by lens
A transparent medium surrounded by two curved surfaces, one or both of whose surfaces are spherical, is called a lens.
There are two types of lenses-
1. convex
2. concave
Convex lens
The two spherical surfaces protruding outward in a lens are called convex lenses. Convex lens thicker in the middle than at the edges. A convex lens converges light rays, hence it is also called a converging lens.

Concave lens
A lens is surrounded by two spherical surfaces curved inwards. Concave lens is thicker at the edges than in the middle.
Such lenses diverge light rays, hence they are also called diverging lenses.

Formation of images from lenses using ray diagram
1. From the object, any ray of light coming parallel to the principal axis, after refraction from the convex lens, will pass through the principal focus on the other side of the lens and in the case of a concave lens, the ray of light appears to diverge from the principal focus on the other side of the lens.


2. The ray of light passing through the principal focus appears to emerge parallel to the principal axis of the lens after refraction from a convex lens and the ray of light that appears to meet at the principal focus of a concave lens appears to emerge parallel to the principal axis after refraction.


3. The ray of light passing through the optical centers of both the lenses passes through its straight path without any deviation after refraction.




Capacity of lens

The ability of a lens to bend rays of light is called the power of a lens.
The power of the lens is expressed as P, its unit is diopter.
1D = 1/m diopter
If the focal length of the lens is f, then the power of the lens is
tan δ = h/f
If,
h=1
tan δ = 1/f
δ = 1/f (small value of δ)
Therefore,
P=1/f
Lens formula and magnification
Just as we found the formula for spherical mirrors, similarly the lens formula has been established for spherical lenses also.
If object distance (u), image distance (v) and focal length (f) are
1/v – 1/u = 1/f
Magnification of a lens is the ratio of height of image to the height of the object. It is denoted by m.
If the height of the object is (h) and the height of the image formed by the lens is (h’), then
m = height of image/height of object
m = h’/h
The magnification produced by a lens is also related to the distance of the object (u) and the distance of the image (v).
Magnification(m) = h’/h
(m) = v/u
Numerical question related to lens
1. The focal length of a concave lens is 15 cm. At what distance should the object be placed from the lens so that an image is formed at a distance of 10 cm from the lens? Also find the magnification produced by lens.
Solution-
A concave lens always forms a virtual, erect image on the same side on which the object is placed.
Reflection distance v = -10 cm
Focus distance f = -15 cm
Object distance u= ?
Formula-
1/v – 1/u = 1/f
1/u = 1/v – 1/u
1/u =(1/-10) – (1/-15)
1/u = (1/-10) + 1/15
1/u = -1/30
u = -30 cm (distance of object)
Magnification, m = v/u
m = -10/-30
m = +1/3
Here the positive sign indicates that the image will be erect and virtual.
2. A 2.0 cm long object is placed perpendicular to the principal axis of a convex lens of focal length 10 cm. The distance of the object from lens to lens is 15 cm. Find the nature and position and the size of the image. Also find its magnification.
Solution–
Height of object h = +2.0 cm
Focus distance f = +10 cm
Distance of object u = -15 cm
Reflection distance v = ?
Image height h’ = ?
Formula_
1/v – 1/u = 1/f
1/v = 1/f + 1/u
1/v = (-1/15 )+ ( 1/10 )
1/v = 1/30
v = +30
The positive sign of v indicates that the image is formed at a distance of 30 cm to the right of the optical center of the lens. The image is real and inverted.
Magnification, m = h’/h = v/u
Or,
Image height h’ = mh
h’ = h(v/u)
h’ = 2(+30/-15)
h’ = 2(-2)
h’ = -4.0 cm
Magnification, m = v/u
m = +30/-15
m = -2 cm
The negative signs of m and h’ indicate that the image is inverted and real. It is formed below the main axis
Thus, a real inverted and 4.0 cm long image will be formed on the right side of the lens at a distance of 30 cm from the lens. This image will be twice the image.
Formation of Rainbow / How Rainbow is formed
When sunlight enters a raindrop, it is refracted along its path, causing different wavelengths of white light.
So the one with higher wavelength (red) bends the least while the one with lower wavelength (violet) bends the most.
After this, these component rays hit the surface inside the drop and if the angle between the normal and the refracted ray on the drop surface becomes more than the critical angle (48°), then the light gets reflected inside the drop itself. This reflected light is refracted again as it exits the drop.
So it is found that violet light is emitted at an angle of 40° and red light is emitted at an angle of 42° with respect to the light ray coming from the Sun. The values of the angles for the wavelengths of other colors lie between the red and violet wavelengths.




[…] Read full chapter….. […]
[…] The angle ∆ between the refracted ray and the incident ray is the angle of deviation In quadrilateral AQNR, ∠A+∠QNR = 180° __________ (1) From ∆QNR, ∠r1+∠r2+∠QNR = 180° ________ (2) From equation (1) and (2) ___ ∠A+∠QNR = ∠r1+∠r2+∠QNR ∠A = ∠r1+∠r2 _________ (3) Since, r1=r2 = r ______ (4) Because, ∠i=∠e Therefore, A = r+r _____(from Eq.(4)) A = 2r = A/2 ______ (5) Since, δ is the sum of deviations on both faces Therefore, δ=( i – r1 )+( e – r2 ) δ= i + e – A ________ (6) Since, δ= δm (deviation angle) From equ. (6) δm = i + i – A _______ ( i = e ) δm = 2i – A i = ( δm + A ) / 2 _______ (7) we know that n = sin i/ sin r n= sin i [(A+ δm)/2] / sin A/2 {From equations (4) and (7)} Read full chapter….. […]
[…] Just as we found the formula for spherical mirrors, similarly the lens formula has been established for spherical lenses also. If object distance (u), image distance (v) and focal length (f) are 1/v – 1/u = 1/f Magnification of a lens is the ratio of height of image to the height of the object. It is denoted by m. If the height of the object is (h) and the height of the image formed by the lens is (h’), then m = height of image/height of object m = h’/h The magnification produced by a lens is also related to the distance of the object (u) and the distance of the image (v). Magnification(m) = h’/h (m) = v/u Read full chapter…….. […]
[…] When sunlight enters a raindrop, it is refracted along its path, causing different wavelengths of white light. So the one with higher wavelength (red) bends the least while the one with lower wavelength (violet) bends the most. After this, these component rays hit the surface inside the drop and if the angle between the normal and the refracted ray on the drop surface becomes more than the critical angle (48°), then the light gets reflected inside the drop itself. This reflected light is refracted again as it exits the drop. So it is found that violet light is emitted at an angle of 40° and red light is emitted at an angle of 42° with respect to the light ray coming from the Sun. The values of the angles for the wavelengths of other colors lie between the red and violet wavelengths. Read full chapter…….. […]
[…] When a traveling ray of light hits a reflective surface, it returns back to the same medium or gets reflected, then this phenomenon is called reflection of light. […]
[…] sunlight travels in the Earth’s circle, it is scattered by the particles in the atmosphere. Light of shorter wavelengths is far more visible than that of larger wavelengths. The amount of […]