Electric capacitance
When a conductor is charged, its potential increases.
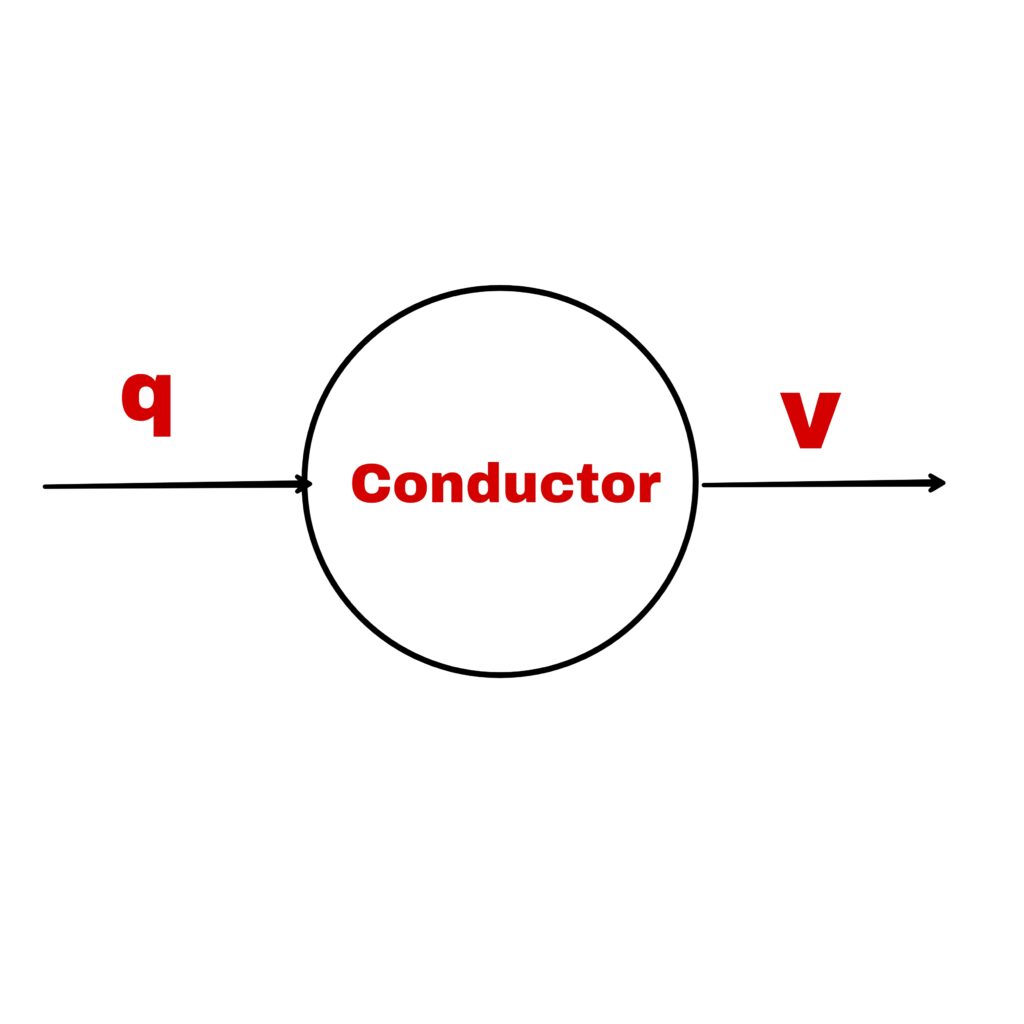
q ∝ V
q= C.V
Where C is a constant.
Which is called the electric capacitance of the conductor.
C=q/V coulomb/volt
Electric capacitance of spherical capacitor
Construct a spherical capacitor whose radius is a and total charge is q. If this charge is considered to be located at the center of the neck, then the potential of the spherical capacitor surface due to this charge
V = [1/4π∈₀].[q/a]
Therefore, the capacitance of spherical capacitor
C= q/V
C= q/[1/4π∈₀].[q/a]
C= 4π∈₀.a
C ∝ a
Since the conductor is in vacuum.
Therefore,
In this case its capacitance is we represent it by Cₒ.
Cₒ=4π∈₀.a ——(1)
When a spherical capacitor is placed in a medium whose dielectric constant is K, then the capacitance of the conductor in this case is
Cₒ=4π∈₀.K.a ——(2)
Equation (2/1)
C/Cₒ = K
C= Cₒ.K
Potential energy of a charged conductor
When a conductor is charged, some work has to be done.
This work gets stored in the charged conductor in the form of electric potential energy.

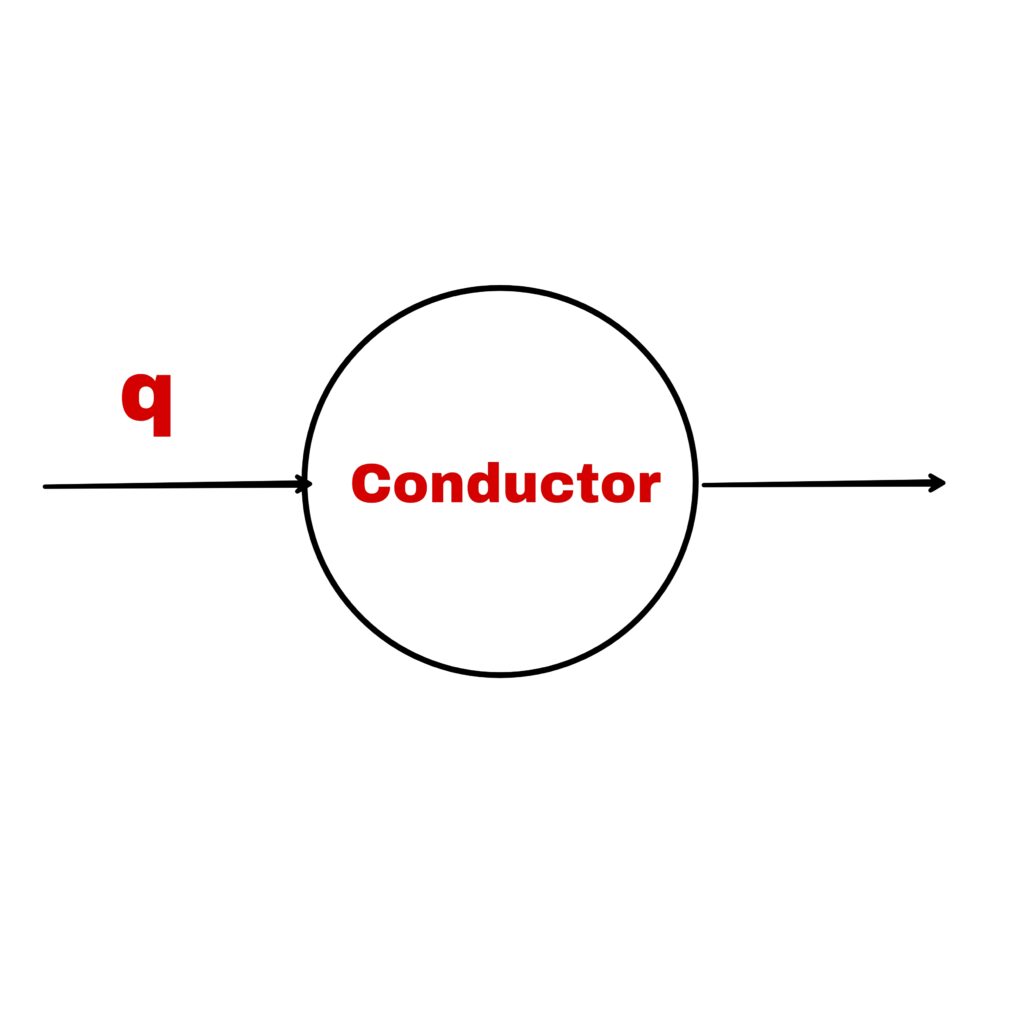
Suppose a conductor whose potential is zero initially.
On giving +q charge, its potential becomes V. Hence,
In this case,
The average potential of the conductor is,
= (0+v)/2
= v/2
Hence,
By the definition of potential the total work done on giving a charge of q to the conductor is
v/2=w/q
w= (v.q)/2
If,
The work is stored in the form of potential energy on the surface of the charged conductor.
Hence the potential energy of the conductor is
U=½(q.v)
U=(q.v)/2
If the capacitance of the conductor is C then
C= q/v
q= c.v
U=½(cv²) joule
If,
v=q/c
Hence,
U=½(q.q/c)
U=½(q²/c) joule
Capacitor
Capacitor is such an arrangement in which sufficient quantity can be stored on a conductor without changing its shape.
“Capacitor is a pair of two conductors of any shape which are near each other and have equal and opposite charge.”
These conductors are called plates of the capacitor.
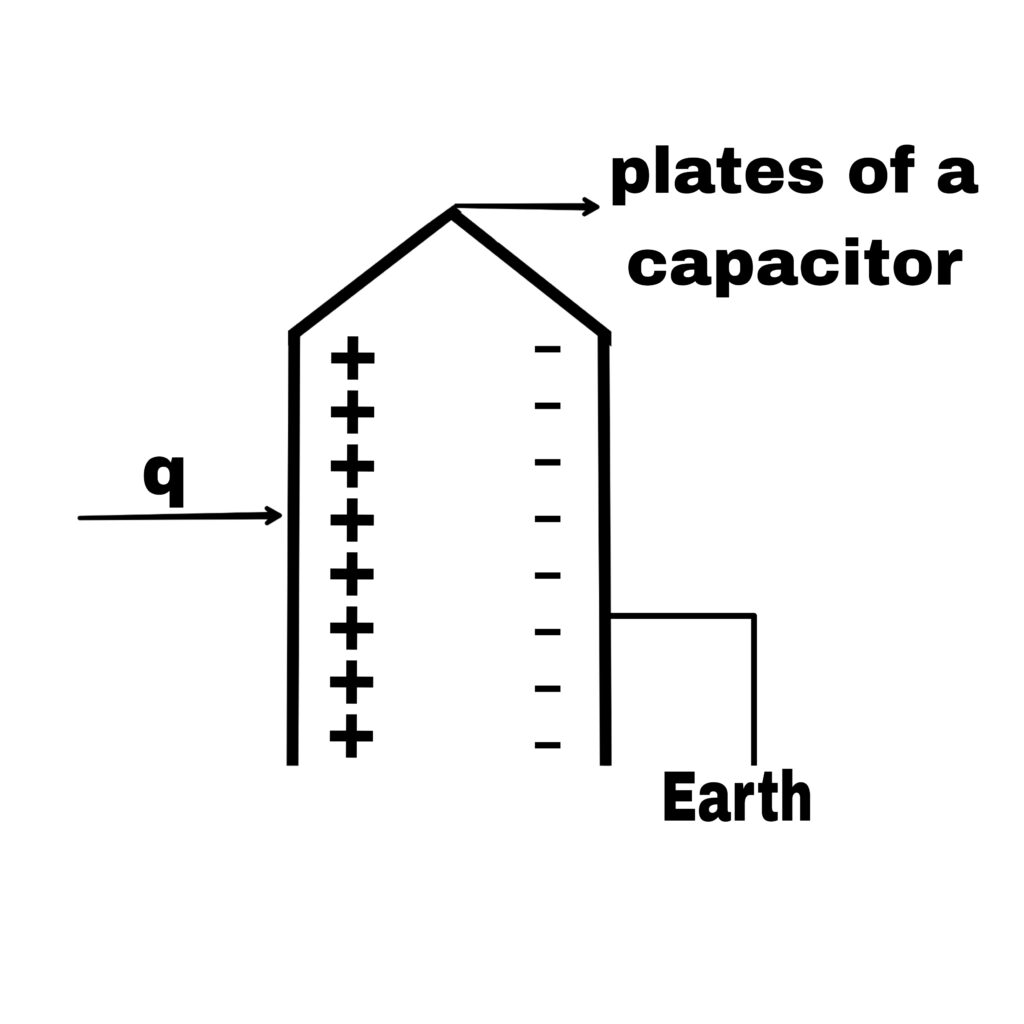
Principle of capacitor
Its principle is based on the fact that when another charged conductor is placed near a charged conductor, the potential of the charged conductor decreases.
If the charged conductor is connected to the earth, its potential decreases even more.
As a result,
The capacitance of the charged conductor increases considerably.
Capacitance of capacitor
If,
The charge on the plates of a capacitor is +q and -q and the potential difference between them is v.
Then the capacitance of the capacitor.
c=q/v
Thus,
The capacitance of a capacitor is the ratio of the charge given to one plate of the capacitor and the potential difference generated between the two plates.
Factors affecting the capacitance of a capacitor
1. On the area of the plates
The capacitance of a capacitor depends on the area of the plates and is proportional to the area
i.e.
C∝A
2. Distance between the plates
The capacitance of a capacitor is inversely proportional to the distance between the plates
C∝1/d
3. On the medium between the plates
The capacitance of a capacitor is proportional to the dielectric constant of the medium between the plates
i.e.
C∝k
Capacitance of a parallel plate capacitor
A parallel plate capacitor mainly consists of two long and flat metal plates which are placed in two electric stands at a short distance from each other. These plates remain parallel to each other and the space between them is filled with air or some dielectric medium.
Let the area of each plate be A meter² and the distance between the plates be d meter².
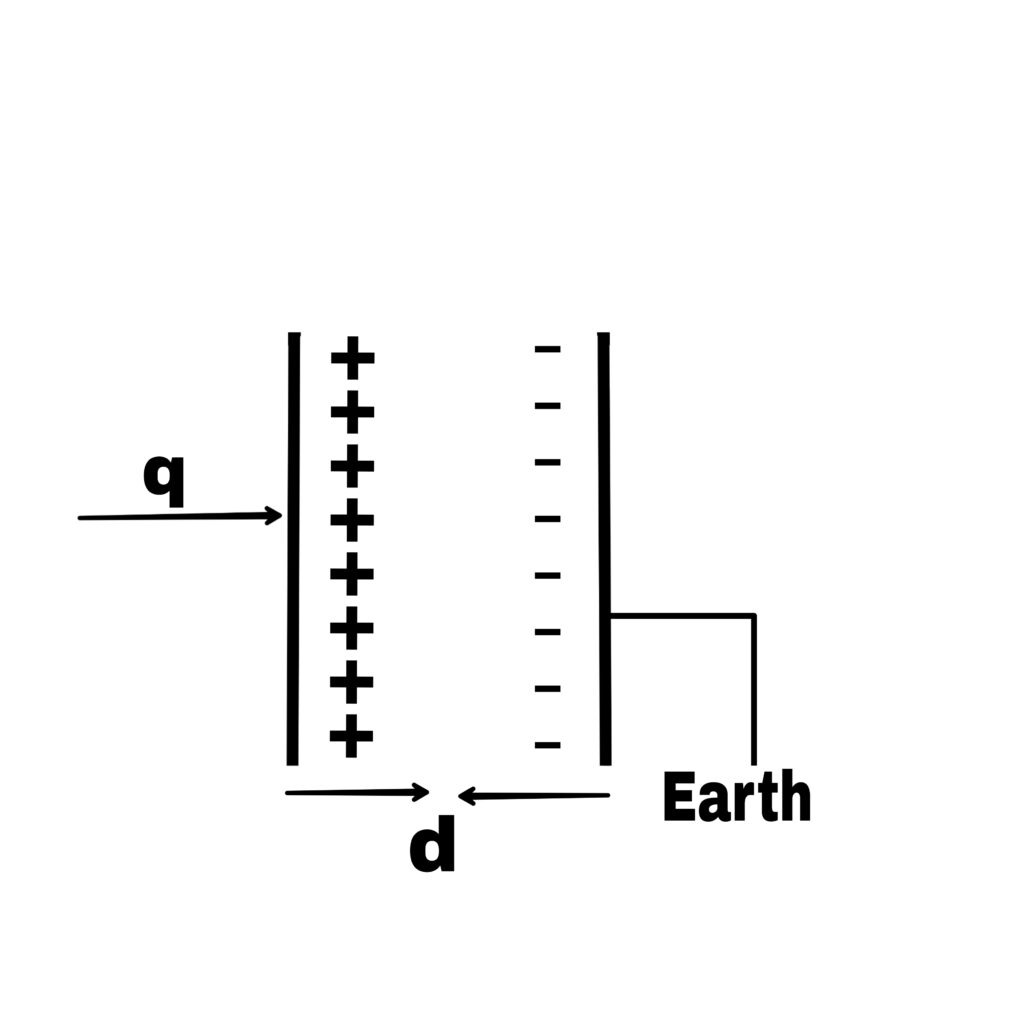
If the surface density of charge on each plate is 𝛿, then the intensity of electric field at any point between the plates is
E = 𝛿/∈₀
Where 𝛿 is the permittivity of vacuum
If there is a dielectric medium between the sheets, then the intensity of electric field is
E = 𝛿/∈₀.k
Where k is the dielectric constant of the medium
𝛿=q/A
Therefore
E= q/(A.∈₀.k)———–(1)
If the potential difference between the two plates was V and the distance between them was d, then the intensity of electric field between the plates is
E = V/d—————(2)
From equations (1) and (2)
q/(A.∈₀.k) = V/d
or,
q/V = (A.∈₀.k).d
If the capacitance of a parallel plate capacitor is C
Therefore,
C = q/V
C = (A.∈₀.k).d————-(3)
If there is vacuum or air between the plates then,
K = 1
In this case the capacitance of the whole plate capacitor
C₀ = (A.∈₀).d———–(4)
From equation (3) and (4)
C = C₀.K
K= C/C₀
Van de Graaff generator
With the help of Van de Graaff generator, very high voltage of the order of 10⁶ volt can be generated.
Its principle is based on two electrostatic phenomena.
1. The electric discharge from a charged conductor into air takes place primarily from its pointed ends.
2. Charge of a hollow conductor is the present on its outer surface.
1. The electric discharge from a charged conductor into air takes place primarily from its pointed ends.
Suppose,
The radius of a sphere is r and it is given a charge of q, then the increase in potential of the spherical conductor due to charging is,
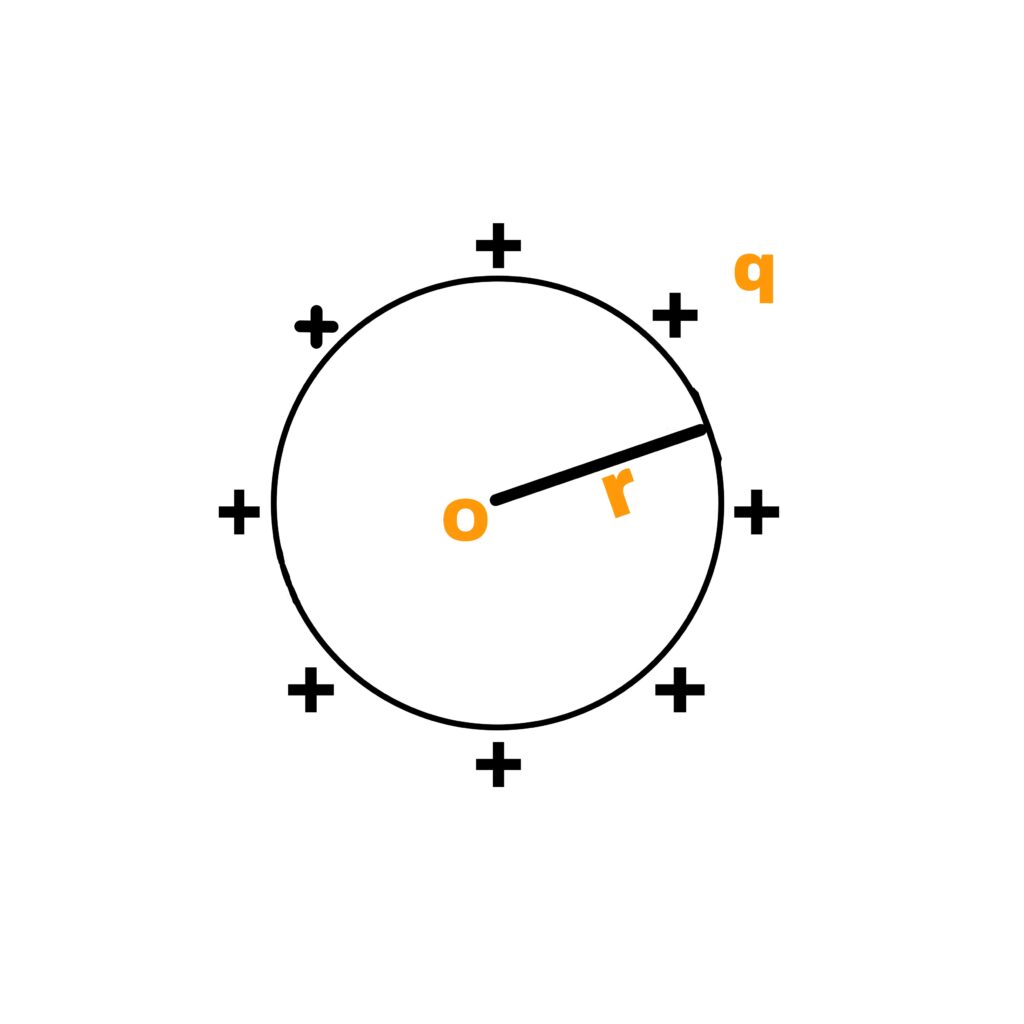
V= [1/4π∈₀][q/r]
q = 4π∈₀r.V
Surface charge density of the throat
𝛿= q/A
𝛿= [4π∈₀r.V]/A
𝛿= [4π∈₀r.V]/4πr²
𝛿= [∈₀.V]/r
𝛿∝1/r
When,
r→0
𝛿→∞
Due to this high charge density, charge will dissipate. Due to which the air particles in contact with the pointed ends take charge and repel each other.
Now new particles come in contact and move away by repelling, due to which a current is formed in front of the charged particles in front of the pointed ends.
2. Charge of a hollow conductor is the present on its outer surface
Suppose,
There is a spherical conductor A of radius r on which there is a charge of +q. It is surrounded by a spherical shell of radius R on which there is a charge of +Q.
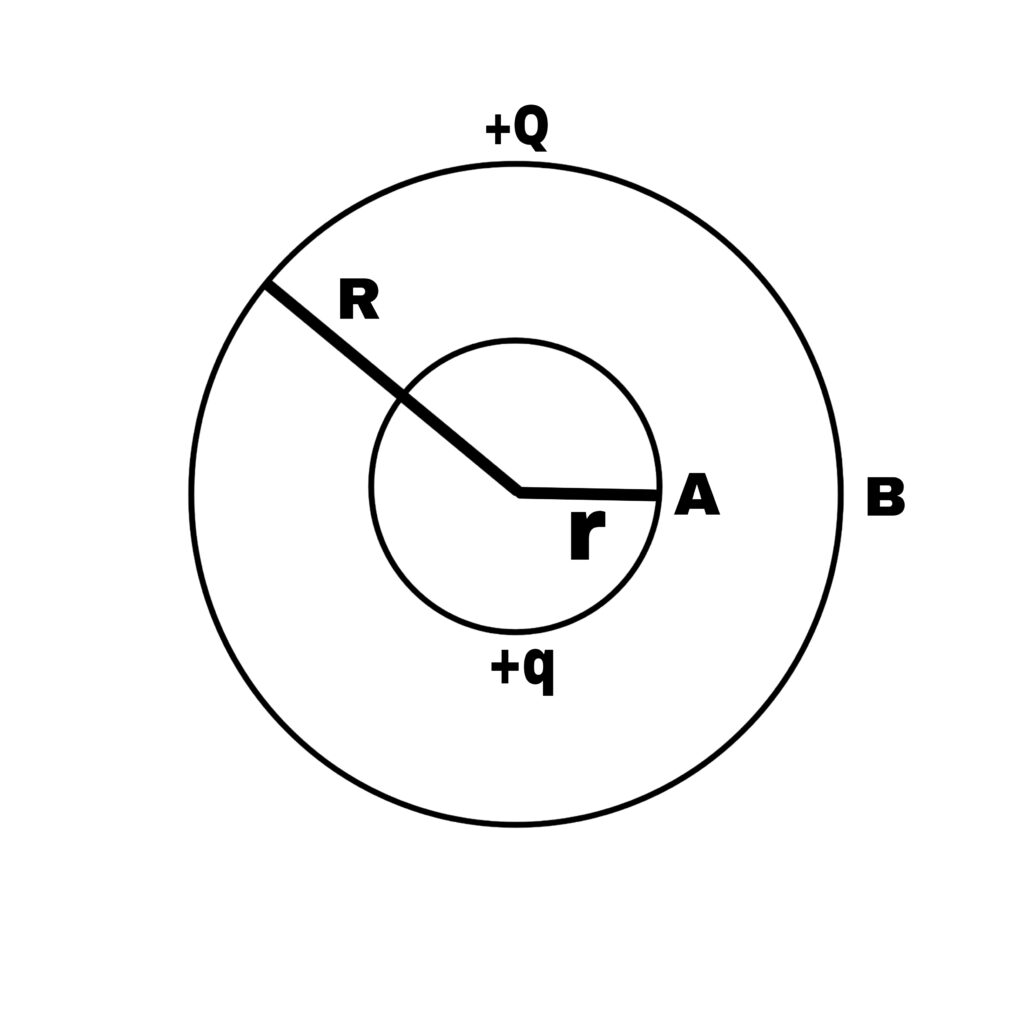
If the charge distributed on the surface of a sphere is considered concentrated at its centre, then the potential of sphere A due to this charge distribution is
VA = 1/[4π∈₀].[q/r]+1/[4π∈₀].[Q/R]
And the potential of sphere B is
VB = 1/[4π∈₀].[Q/R]+1/[4π∈₀].[q/R]
Or,
Potential difference between sphere A and shell B
VA-VB = q/4π∈₀[1/r – 1/R]
It is clear from the above equation that VA-VB does not depend on the charge of shell B whether it is positively charged, negatively charged or uncharged. And
VA-VB > 0
If q is positive
R > r
Thus,
If we connect the small and the big sphere with a wire, then the charge will immediately flow from the small sphere to the big sphere.
Construction
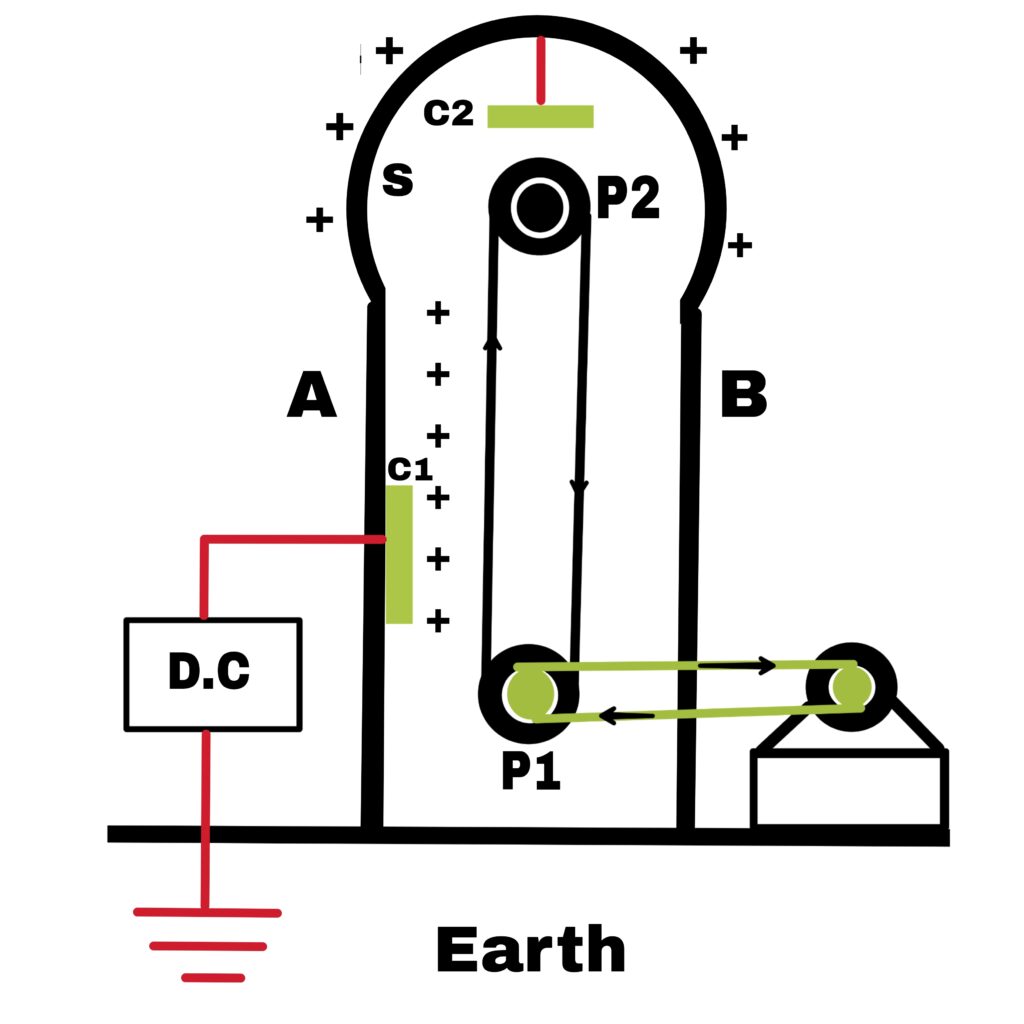
A large metallic sphere is fixed on two support pillars and it has a rubber or silk headless belt which can be run on two pulleys P1 and P2 with the help of an electric motor.
The lower comb C1 is connected to positive terminal of very high voltage source D.C and upper comb C2 is connected to inner surface of the hollow sphere S.
Working method
When very high voltage is applied to the comb C1, it generates ions as a result of the action of sharp points or in its place.
Due to repulsion b/w the cations and the comb C1, these cations move on the belt.These ions are taken up by the moving belt. The sharp ends of C2 touch the belt exactly.
Due to which the comb C2 collects the positive charge of the belt.
Whereby the positive charge is soon transferred to outer surface of the sphere S. Thus the belt keeps rotating. Its surface continuously receives positive charge and its potential becomes very high. When the sphere S potential becomes very high and the dielectric strength of the nearby air breaks down and the charge is dissipated in the nearby air.
At maximum potential, the rate of dissipation of the charge becomes equal to the rate of the charge transferred to the sphere S.

[…] Specific resistance or resistivity Derivation of ohm’s law Electrical current and Ohm’s Law Van De Graaff Generator Working And Derivation Electric capacitor and capacitance […]
[…] determine the magnetic field produced by a serial conductor, Biot-Savart first divided the serial conductor into equal small […]