Function of simple microscope
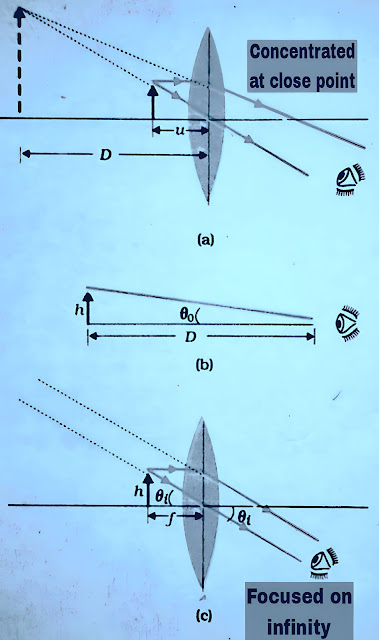
A simple magnifier or simple microscope has a converging lens of short focal length. To use this type of lens as a microscope, the lens is placed near the object at one focal length or less than the focal length and on the other hand the eye is kept close to the lens, by doing this the object is seen directly. The magnified and virtual image should be formed at such a distance that the eye can see it easily, that is, the image should be formed at a distance of 25 cm or slightly more.
If the object is placed at f then its image is formed at infinity and if the object is placed at a distance less than f then the image is virtual and at a distance less than infinity. Therefore, the nearest comfortable distance for viewing is at the near point (distance D = 25cm), but this has some effect on the eye, hence the image formed at infinity is considered suitable for viewing by the eyes.
The angle subtended by the image at the eye and the object at a distance u is
The angle subtended at the eye by the image from h’/h = m = v/u
tanθ = h’/-v
tanθ = h’/-v = (h/-v)(v/u) = h/-u ≈ θ
The angle subtended by the object, while the object is now at u=-f
qi = h/f
m = (qᵢ/qₒ)
m = D/f
This is one less magnification than the position at which the image is formed at the near point, Eq. (1), but viewing the image is relatively more comfortable and the difference in magnification is also relatively small.
Function of compound microscope
A simple microscope has a high magnification (≤9) for lenses of real focal lengths. For greater magnification, two lenses are used in which one lens combines (enhances) the effect of the other lens.
This is called compound microscope. The lens closest to the object is called objective which forms the real, inverted and magnified image of the object. This image acts as an image for the second lens. This lens is called eye-piece.
Which actually works as a simple microscope or magnifier and the final magnified virtual image is formed. Thus the first inverted image occurs near or inside the focal point of the eyepiece, at a distance from the eyepiece that is suitable for forming the final image at infinity.
The ray diagram shows that the linear magnification due to the objective is equal to h’/h.
mₒ = h’/h = L/fₒ ———(1)
This quantity has been used,
tanθ = (h/fₒ) = (h’/L)
Here h’ is the size of the first image and size of the object is h and focal length of the objective is fₒ. The first image formed near the focal point of the eyepiece. The distance L, i.e., the distance between the second focal point of the objective and the first focal point of the eyepiece (focal distance fe) is called the tube length of the compound microscope.
Because the first inverted image is formed near the focal point of the eyepiece.
Angular magnification,
mₑ = (1+D/fₑ)
When the image is formed at infinity then the angular magnification due to the eyepiece is,
mₑ = D/fₑ ———(2)
Hence total magnification
m = mₒ.mₑ =(L/fₒ) (D/fₑ)
From equation (1) and (2).
Example
What will be the magnification of the compound microscope for an objective of
fₒ = 1cm, eyepiece of fₑ = 2cm and tube length L = 20cm? (D=25 cm)
Solution
m = mₒ.mₑ= (L/fₒ) (D/fₑ)
m = (20/1)(25/2)m = 20 × 25/2
m = 250 D

