Huygen's wave theory

Huygen's Principle

When we throw a small stone in a calm water pond, waves propagate around the rebound point. Every point on the surface starts oscillating with time. The photograph of the page at any given moment will show the circular rings above which the disturbance is maximum. Apparently, all the points in this type of circle oscillate in the same art as they are equally spaced from the source.

The point path of all such points oscillating in the same art is called the waveform. Therefore, a waveform is defined as the surface of similar art. The speed with which the waveform moves out of the source is called the speed of the wave. The energy of the wave moves perpendicular to the wavelength.

If a point-source emits uniform waves in every direction, then the point path of the points, which have the same amplitude and which vibrate in the same art, is a sphere and we get a spherical wave like that.

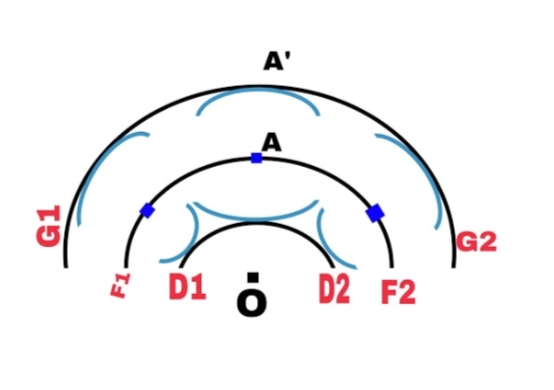
Now if we know the shape of a waveform at t= 0, then by the principle of Huygens we can find the shape of the waveform at a later time τ. Thus, the principle of Huygens is actually a geometrical design that if at some point in time the shape of the waveform is given, then at some later time we can find the shape of the waveform. If a divergent wave F1F2 represents a portion of a spherical waveform at time t=0.

Now according to Huygens's theory, each point of the waveform is the source of a secondary disturbance and the nerves from these points propagate in all directions at the speed of the wave. In this wavelets emanating from wavelet are often known as secondary wavelets and if we draw a common tangent surface on all these circles, we get a new position of the waveform at a later time.

Therefore, if we want to find the shape of the wavelength at t = τ time, we will draw a circle of radius vτ from each point of the spherical wavelet, where the medium represents the speed of the wave. If we draw a common tangent line on all these spheres, we get a new position of the wavelength at time t=τ. The new waveform displayed by G1G2 is spherical with a center of 0.

The above model has a flaw. We also get a back wave which is represented by D1D2. Huygens argued that the secondary wavelets have a maximum amplitude in the forward direction and zero in the backward direction. By this ad hoc imagination, Huygens was able to explain the absence of back waves. However, this ad hoc hypothesis is not satisfactory and the absence of backward waves can actually be justified by a more precise wave theory

Refraction of plane waves using Huygens's theory--

Let PP 'is the surface separating mediums 1 and 2 and V1 and V2 are the time taken to cover the distance between the waveform and BC.

BC = V1t

AE = V2t

∆ABC and ∆AEC

Sini=BC/AC

Sinr=AE/AC

Sini=V1t/AC _______ (1)

Sinr=V2t/AC _______ (2)

Here i and r are the incidence and incidence angles of refraction respectively.

Sini/Sinr=V1t/V2t

Sini/Sinr=V1/V2

Therefore,

n1=C/V1,

n2=C/V2

n1 and n2 are the refractive indexes of mediums 1 and 2.

We know that

n1sini=n2sinr

sini/sinr=n2/n1

This is Snell's law of refraction. If λ1 and λ2 represent the wavelength of light in medium 1 and medium 2, respectively, and if the distance BC is equal to λ1 then the distance AE will be equal to λ2.

Therefore,

λ1 / λ2 = V1 / V2

Reflection of plane waves -

Now, on a reflective surface, MN is a plane wave AB incident at any angle i.

If v represents the speed of the wave in the medium and τ represents the time taken by the traverse to move from point B to C.

Then distance

BC = vτ

Let the radius v point from point A to form the reflected waveform and CE represent the tangent plane drawn from point C on this sphere.

So,

AE = BC = vτ

From the triangles EAC and BAC we will find that these two are congruent.

The angle I and angler will be equal.

(This is the law of reflection.)