refraction of light through a prism equation

Refraction of light through a prism 

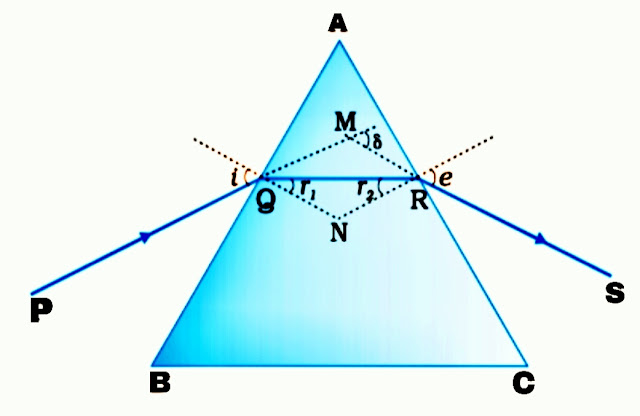
In the prism, the angle of incidence on the first face AB is i and the angle of refraction is r1, while the angle of incidence on the second face AC is r2 and the angle of refraction or exit angle is e.

The angle ∆ between the refracted ray and the incident ray is the angle of deviation

In quadrilateral AQNR,

∠A+∠QNR = 180° __________ (1)

From ∆QNR, ∠r1+∠r2+∠QNR = 180° ________ (2)

From equation (1) and (2) ___

∠A+∠QNR = ∠r1+∠r2+∠QNR

∠A = ∠r1+∠r2 _________ (3)

Since,

r1=r2 = r ______ (4)

Because,

∠i=∠e

Therefore,

A = r+r _____(from Eq.(4))

A = 2r = A/2 ______ (5)

Since,

δ is the sum of deviations on both faces

Therefore,

δ=( i - r1 )+( e - r2 )

δ= i + e – A ________ (6)

Since,

δ= δm (deviation angle)

From equ. (6)

δm = i + i – A _______ ( i = e )

δm = 2i – A

i = ( δm + A ) / 2 _______ (7)

we know that

n = sin i/ sin r

n= sin i [(A+ δm)/2] / sin A/2

{From equations (4) and (7)}