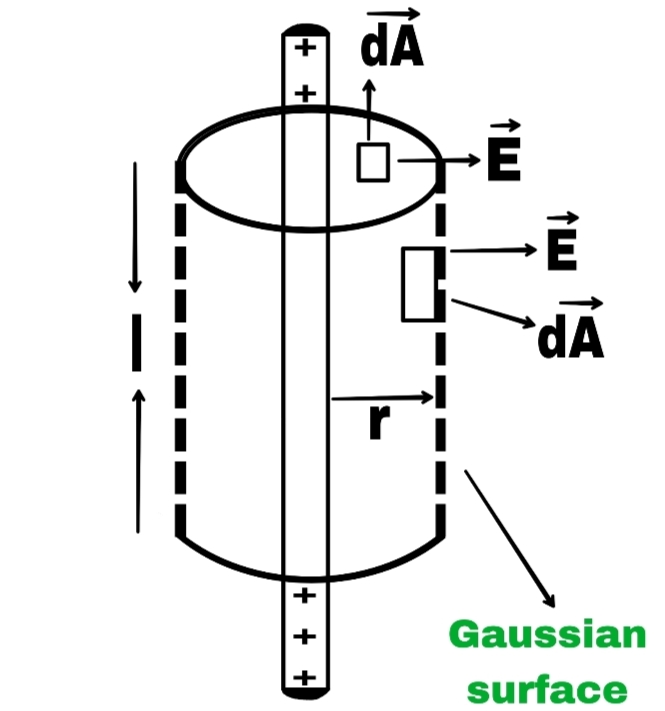
Intensity of the electric field due to uniformly distributed charge on a wire of infinite length.
Or,
Intensity of the electric field near a uniformly charged straight wire of infinite length.
Suppose a charge is uniformly distributed on a line of length l.
If linear density of the distributed charge is λ,
Then the linear density is,
λ=q/l
Suppose there is a point p at a distance r from the wire, where the electric field intensity is to be found.
To find the electric field intensity at point P, draw a Gaussian cylindrical surface of radius r and length l.
Thus, the electric flux passing through the area element dA of the Gaussian surface.
dΦₑ = →E.→dA
dΦₑ = E.dA.Cosθ
dΦₑ = E.dA
Or,
Total electric flux passing through Gaussian surface,
Φₑ= ∫ₐE.dA
Φₑ= E ∫ₐdA
q/∈₀ = E(2πrl)
E= q/(2π∈₀rl)
E= λ/2π∈₀r [ λ=q/l ]
Similarly,
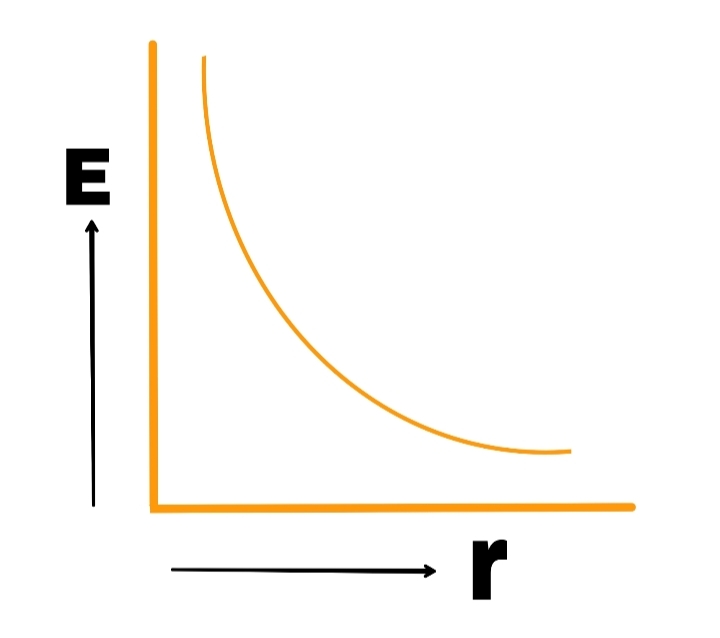
Electric field intensity E due to a linear charge is inversely proportional to the distance r from the point of linear charge.
Gauss’s law
According to this law,
The electric flux Φₑ passing through a closed surface is 1/∈₀ times the total charge q enclosed by that surface.
That is, total electric flux
Φₑ = q/∈₀
where ∈₀ is the permittivity of vacuum
or,
Φₑ =∮→E.→dA
Φₑ= q/∈₀ Gauss’s theorem in integral form.
Where,
∈₀ is the permittivity of vacuum.
Proof –
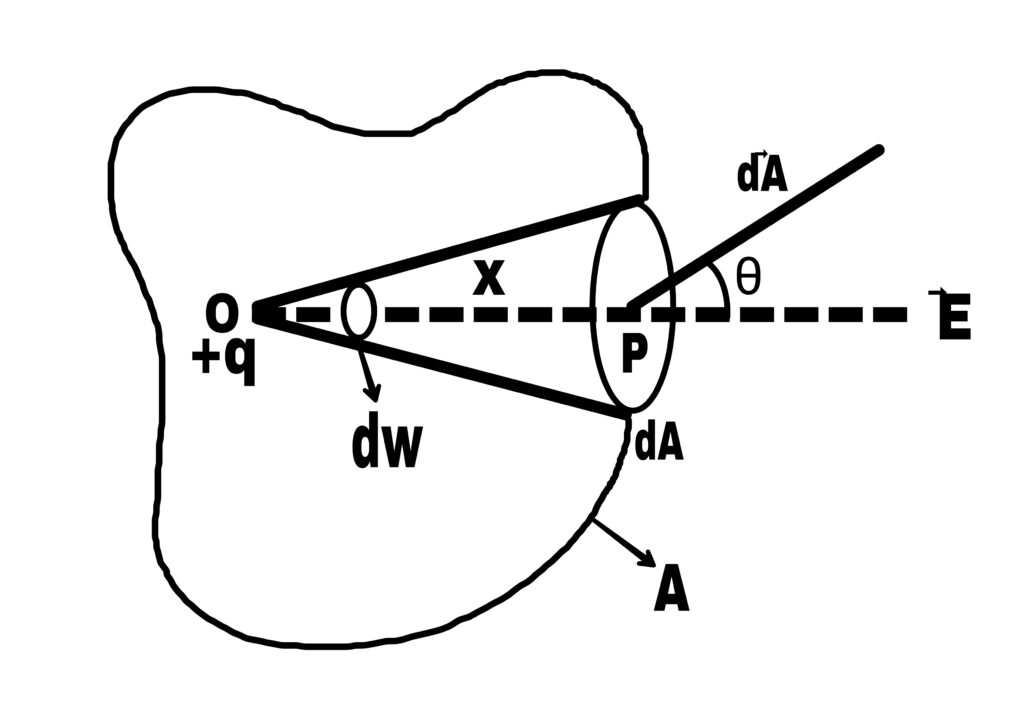
Let a point charge +q be located at point O within a closed surface A. On this surface, there is a small area component dA around the point P.
Let OP = r
The electric field E at a point P due to the charge +q placed at point O is along OP.
Hence, the relation between area component dA and electric flux is
dΦₑ =→E.→dA
dΦₑ = E.dA.Cosθ
Where θ = is the angle between →E and →dA.
or
dΦₑ = [1/4π∈₀][q/r²]dA.Cosθ
dΦₑ = [q/4π∈₀][dA.Cosθ/r²]
dAcosθ = dw→ positive angle
dΦₑ = [q/4π∈₀].dw
Electric flux related to whole surface
Φₑ = [q/4π∈₀].∮dw
Therefore,
∮dw = 4π
Φₑ = [q/4π∈₀].4π
Φₑ = q/∈₀