Intensity of electric field near a charged plane sheet of infinite extension
Suppose that on one surface of a uniformly charged flat sheet of infinite extension whose surface density is δ.
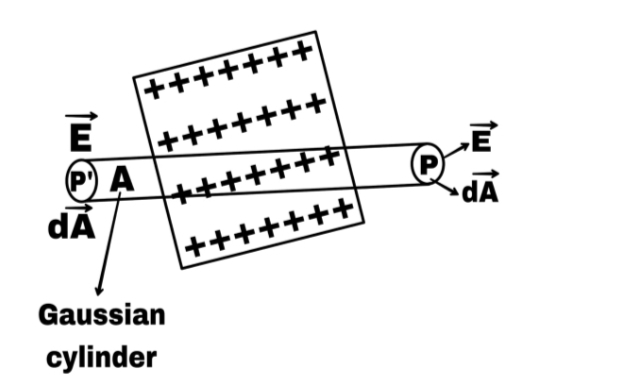
Near a positively charged flat sheet of infinite extension, there is a point P at a distance r from the sheet at which the electric field intensity is to be calculated.
Suppose that, point P’ is the intersection of point P on the other side of the sheet, We imagine a Gaussian cylinder across the sheet whose flat ends are parallel to the sheet and pass through points P and P’.
If area of each end of this cylinder is A, then electric flux passing through both ends of the cylinder is,
Φₑ=∫ₐ→E.→A+∫ₐ→E.→A
Φₑ=∫ₐE.dA.cos0°+∫ₐE.dA.cos0°
Φₑ=2∫ₐE.dA
Φₑ=2E∫ₐdA
Φₑ=2EA——-(1)
But by Gauss’s theorem,
Φₑ = q/∈₀
Where q= is the total charge enclosed by the Gaussian cylinder.
Hence,
q=δ.A (δ=q/A)
Φₑ = q/∈₀
Φₑ=δ.A/∈₀——-(2)
From equation (1) and (2)
2E.A=δ.A/∈₀
E=δ/2∈₀

[…] If the potential difference between the ends of the conductor is v and the current flowing in the conductor is i, then the intensity of electric field […]