Gauss’s law
According to this law,
The electric flux Φₑ passing through a closed surface is 1/∈₀ times the total charge q enclosed by that surface.
That is, total electric flux
Φₑ = q/∈₀
where ∈₀ is the permittivity of vacuum
or,
Φₑ =∫Φ→E.→dA = q/∈₀Gauss’s theorem in integral form.
Φₑ = q/∈₀
Where ∈₀ is the permittivity of vacuum.
Proof –
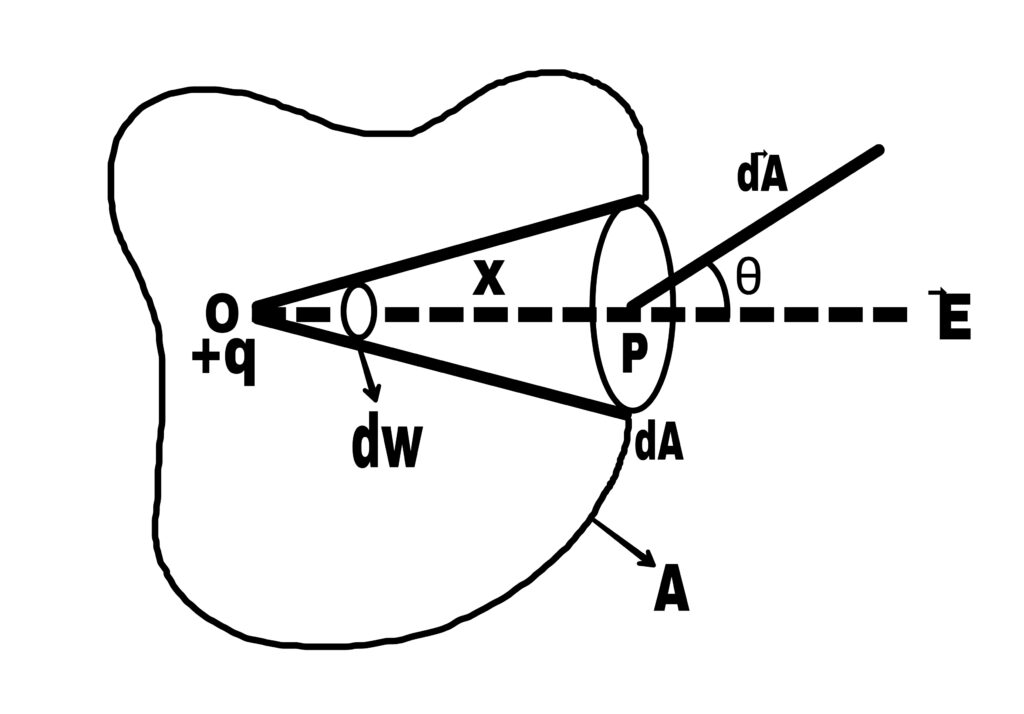
Let a point charge +q be located at point O within a closed surface A. On this surface, there is a small area component dA around the point P.
Let OP = r
The electric field E at a point P due to the charge +q placed at point O is along OP.
Hence, the relation between area component dA and electric flux is,
dΦₑ = →E.d→A
dΦₑ = E.dA.Cosθ
Where θ = is the angle between →E and d→A.
or,
dΦₑ = [1/4π∈₀][q/r²]dA.Cosθ
dΦₑ = [q/4π∈₀][dA.Cosθ/r²]
dAcosθ = dw→ positive angle
dΦₑ = [q/4π∈₀].dw
Electric flux related to whole surface
Φₑ = [q/4π∈₀].∮dw
Therefore, ∮dw = 4π
Φₑ = [q/4π∈₀].4π
Φₑ = q/∈₀
Application of Gauss theorem
Intensity of the electric field due to uniformly distributed charge on a wire of infinite length.
Or,
Intensity of the electric field near a uniformly charged straight wire of infinite length.
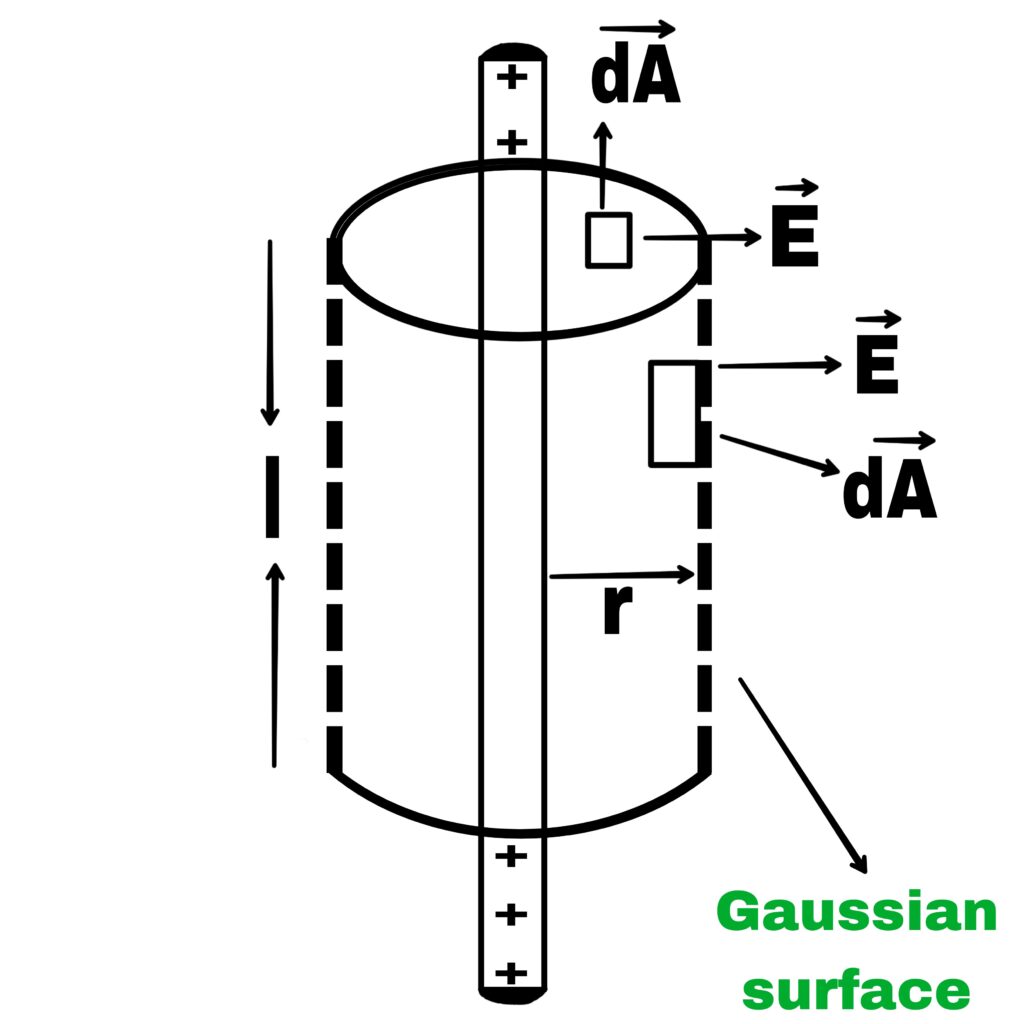
Suppose a charge is uniformly distributed on a line of length l.
If linear density of the distributed charge is λ,
Then the linear density is,
λ=q/l
Suppose there is a point p at a distance r from the wire, where the electric field intensity is to be found.
To find the electric field intensity at point P, draw a Gaussian cylindrical surface of radius r and length l.
Thus, the electric flux passing through the area element dA of the Gaussian surface.
dΦₑ = →E.→dA
dΦₑ = E.dA.Cosθ
dΦₑ = E.dA
Or,
Total electric flux passing through Gaussian surface,
Φₑ= ∫ₐE.dA
Φₑ= E ∫ₐdA
q/∈₀ = E(2πrl)
E= q/(2π∈₀rl)
E= λ/2π∈₀r [ λ=q/l ]
Similarly,
Electric field intensity E due to a linear charge is inversely proportional to the distance r from the point of linear charge.
The intensity of the electric field outside the charged conductor
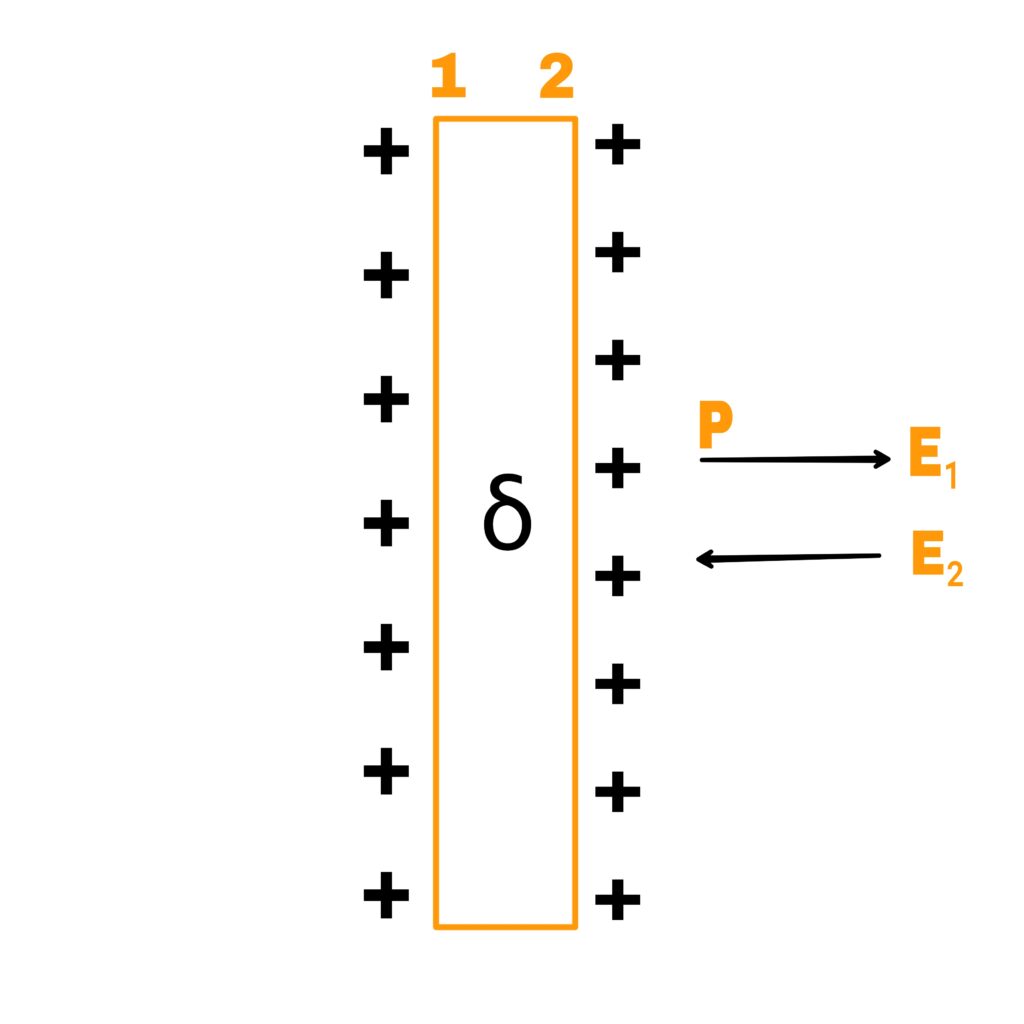
Let us assume a charged plane conductor with the surface density δ. We have calculate intensity of electric field at point p due to this charged conductor. This charged conductor can be considered equivalent to two plane sheets of charge 1 and charge 2.
So, electric field intensity at point p due to sheet 1 is,
E₁= δ/2∈₀
Similarly, electric field intensity at point p due to sheet 2 is,
E₂= δ/2∈₀
Since E₁ and E₂ are in the same direction.
So, the resultant electric field intensity at point P is,
E= E₁+E₂
E= δ/2∈₀ + δ/2∈₀
E= δ/∈₀
The electric field intensity between outside positively and negatively charged parallel insulator plates of equal surface density
Let us assume that there are two large plane non-conductor plates 1 and 2 which are positively and negatively charged respectively. They are placed face to face parallel to each other and charge density on the plate is δ.
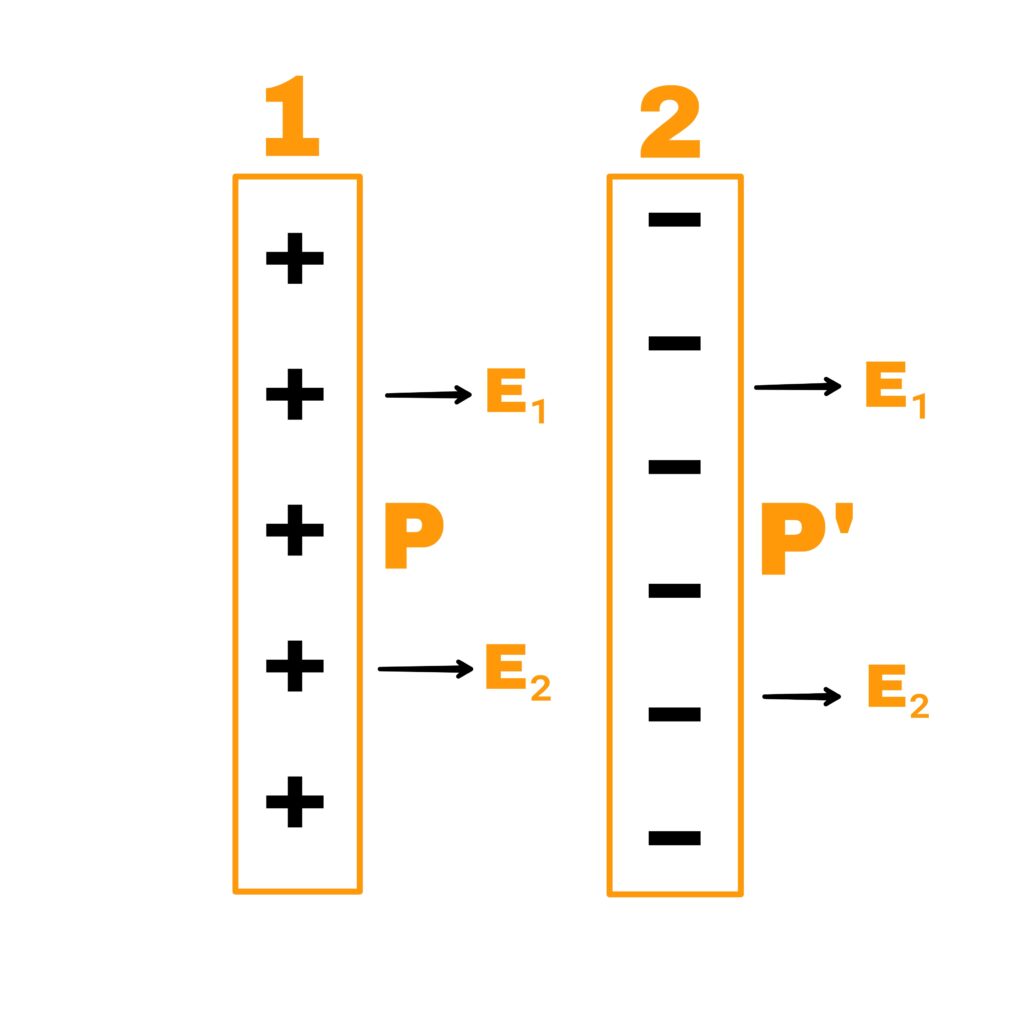
Case 1 – Intensity of electric field between plates
Intensity of electric field due to plate 1,
E₁= δ/2∈₀
Similarly,
The intensity of electric field due to plate 2,
E₂= δ/2∈₀
Therefore, intensity of resultant electric field at P between plates
E= E₁+E₂
E= δ/2∈₀ + δ/2∈₀
E= δ/∈₀
Case 2 – Intensity of electric field outside the plate
Intensity of the electric field at point P outside the plate
E= E₁-E₂
E= δ/2∈₀ – δ/2∈₀
E= 0
The intensity of the electric field due to a uniformly charged spherical shell
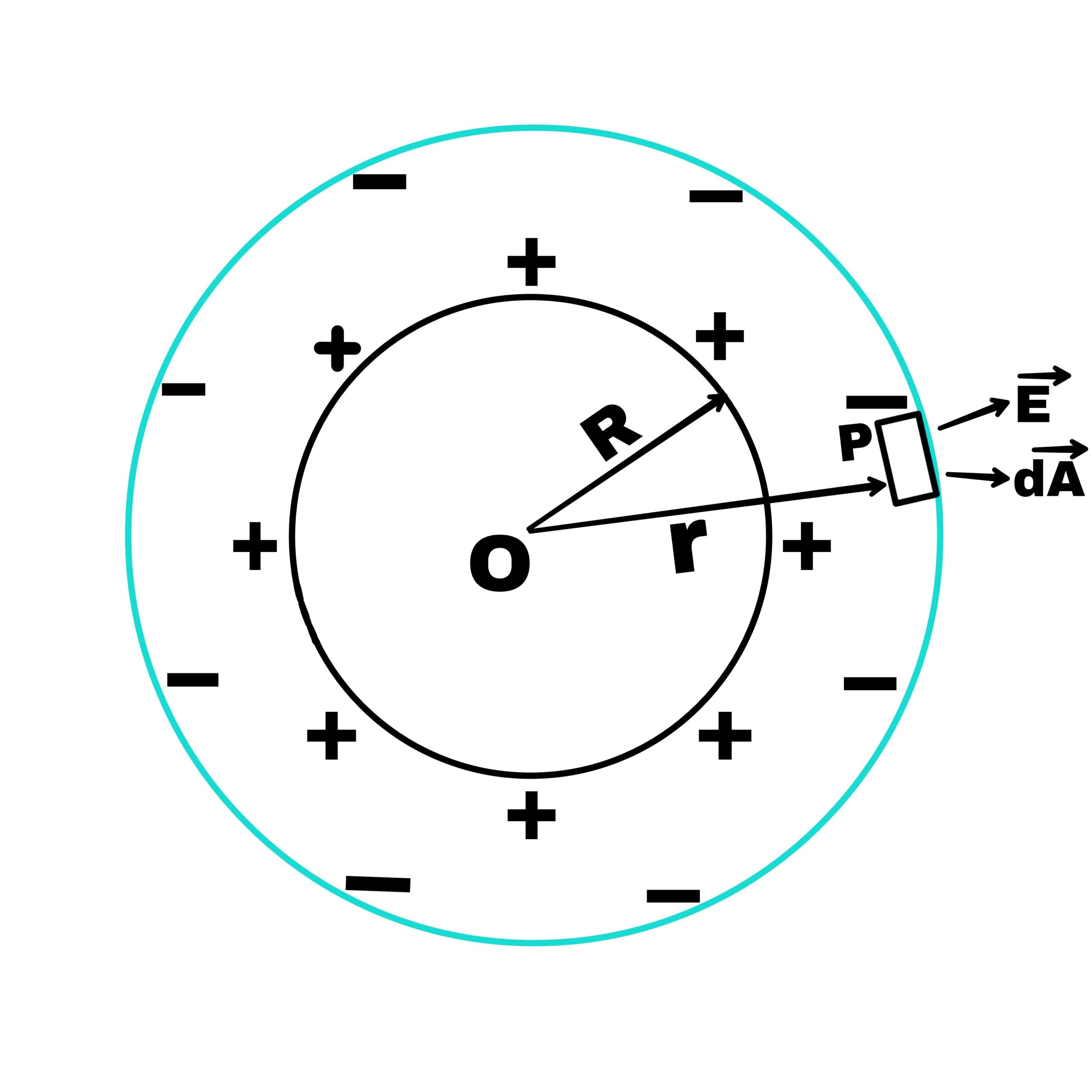
Let us assume an isolated spherical shell of radius r on which charge +q is the uniformly distributed. We have to find the intensity of the electric field outside this shell, on the surface of the shell and inside the shell.
Case 1 – At an external point
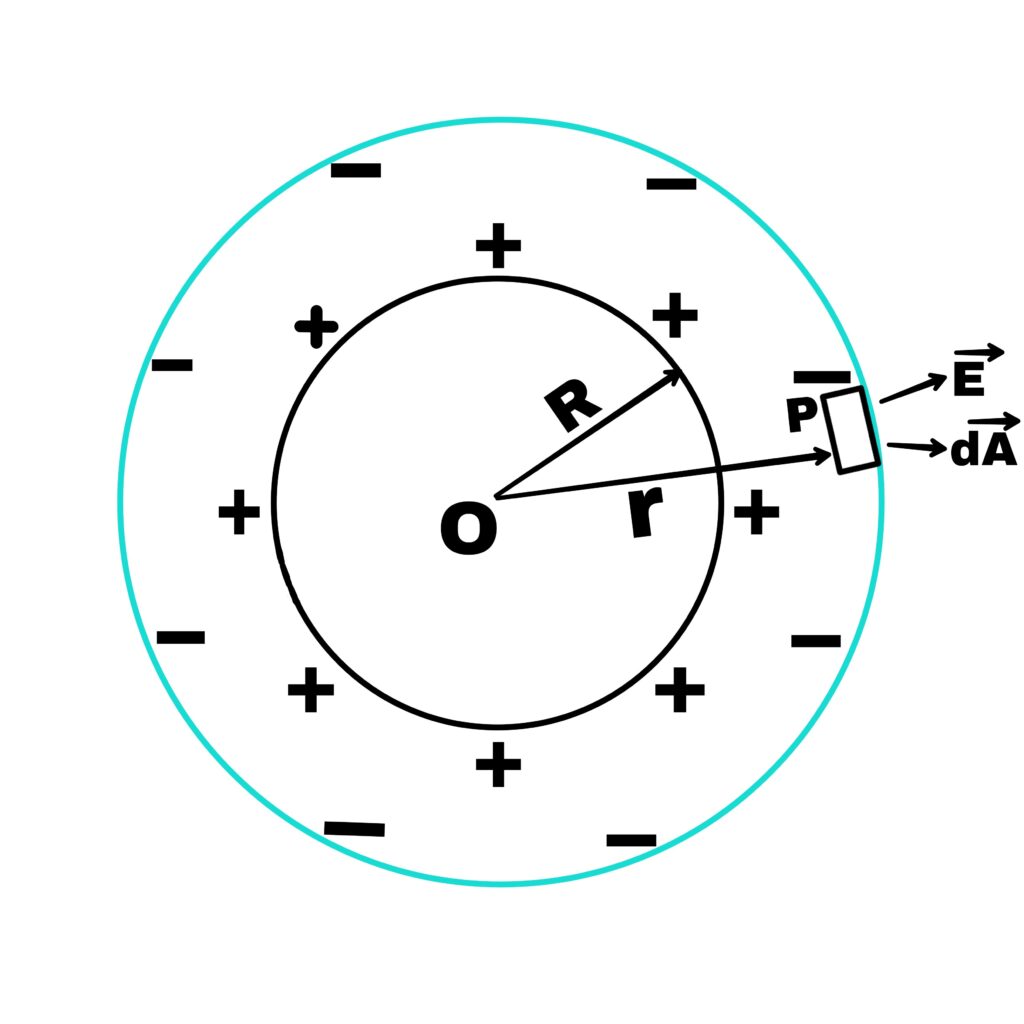
Let a point P be the located at a distance r from the centre O of the spherical shell.
To find the intensity of the valid field at point P, draw a Gaussian spherical surface of radius r.
The flask associated with area dA of this spherical Gaussian surface is,
dΦₑ=→E.→dA
dΦₑ=E.dA.Cosθ
dΦₑ=E.dA.1
dΦₑ=E.dA
Hence, the electric flux passing through the entire Gaussian surface is,
Φₑ= ∮E.dA
q/∈₀= E∮dA
q/∈₀= E(4πr²)
E= (1/4π∈₀).q/r²—–(1)
If surface density of charge on the shell is δ,
then,
δ=q/4πR²
δR²=q/4π
Hence the intensity of the electric field
E= δR²/∈₀r²——(2)
Case 2 – If point P is located on the surface of the shell
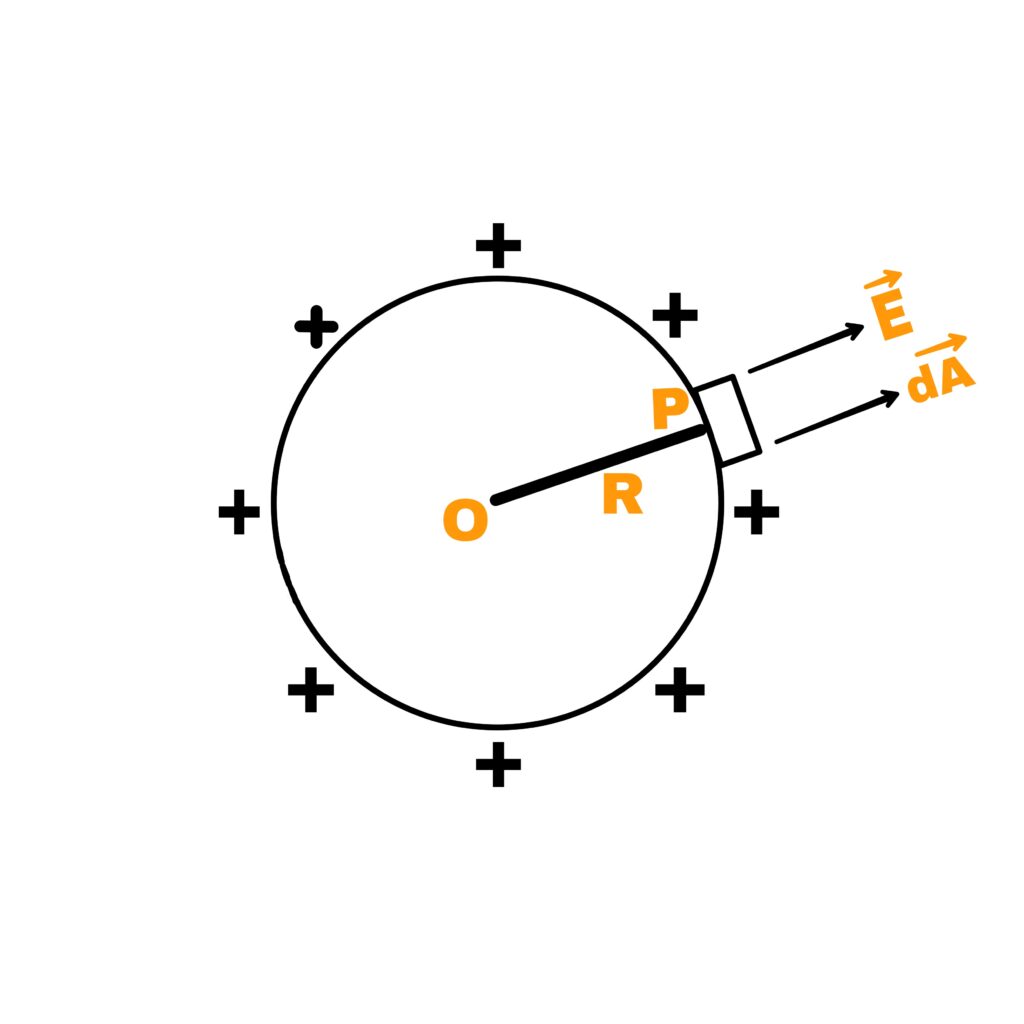
If point P is located on the surface of the shell, then the intensity of the electric field will be known by putting r=R in equations 1 and 2
E= (1/4π∈₀).q/R²
E= δR²/∈₀R²
E= δ/∈₀
Case 3 – At the internal point of the shell
No charge is associated with the Gaussian surface of radius r,
or, (r≺R)
Hence,
∮E.dA= 0/∈₀
∮E.dA= 0
E∮dA= 0
E= 0
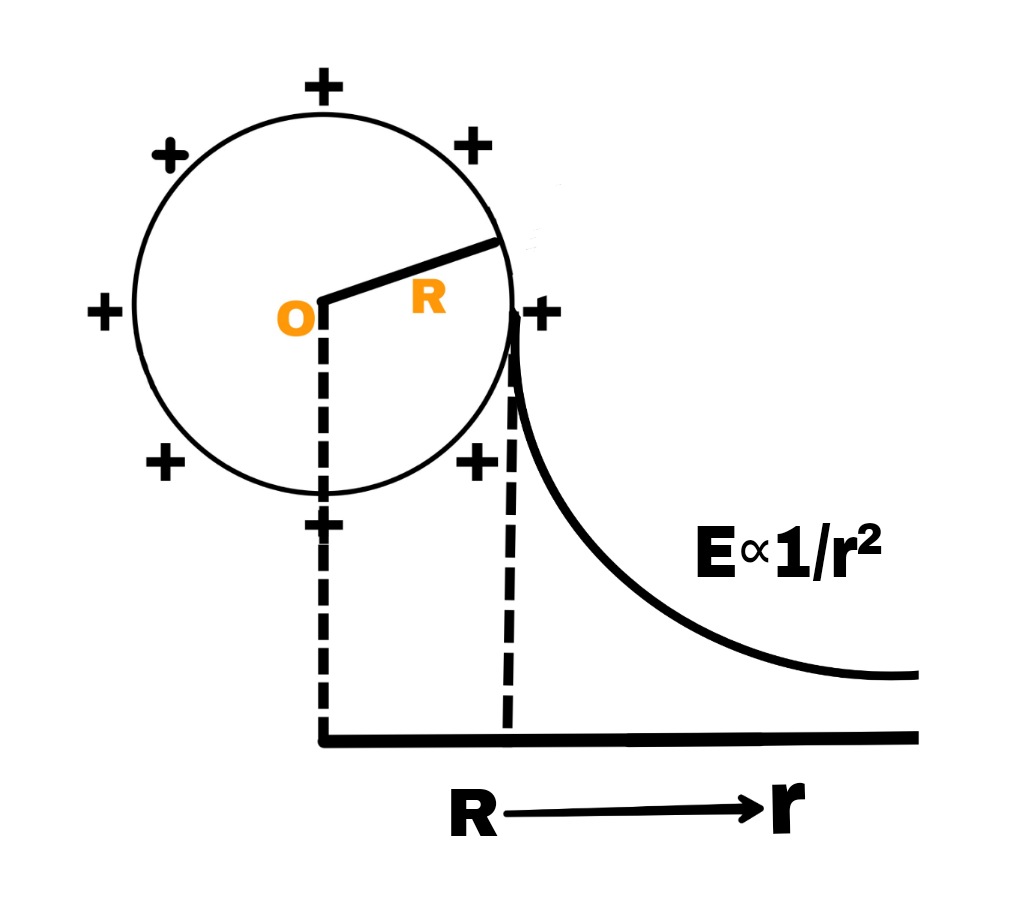
Hence the electric field intensity inside the charged spherical shell is zero everywhere.
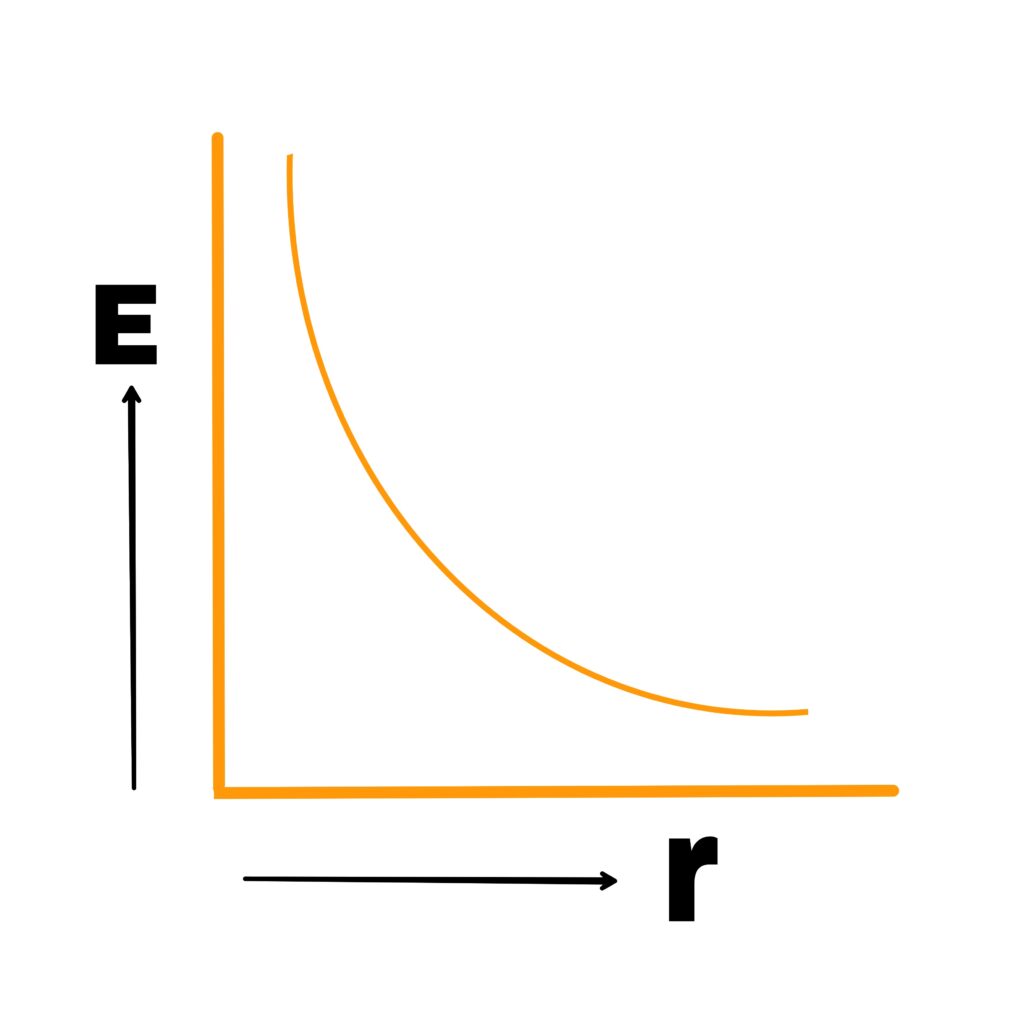
variation of electric field intensity with distance can be shown as follows
It is clear from the figure that inside the shell (from r = 0 to R) the electric field E is zero everywhere and the electric field is maximum on the surface of the shell and the electric field intensity outside the shell decreases rapidly according to the inverse square law.
Intensity of electric field near a charged plane sheet of infinite extension
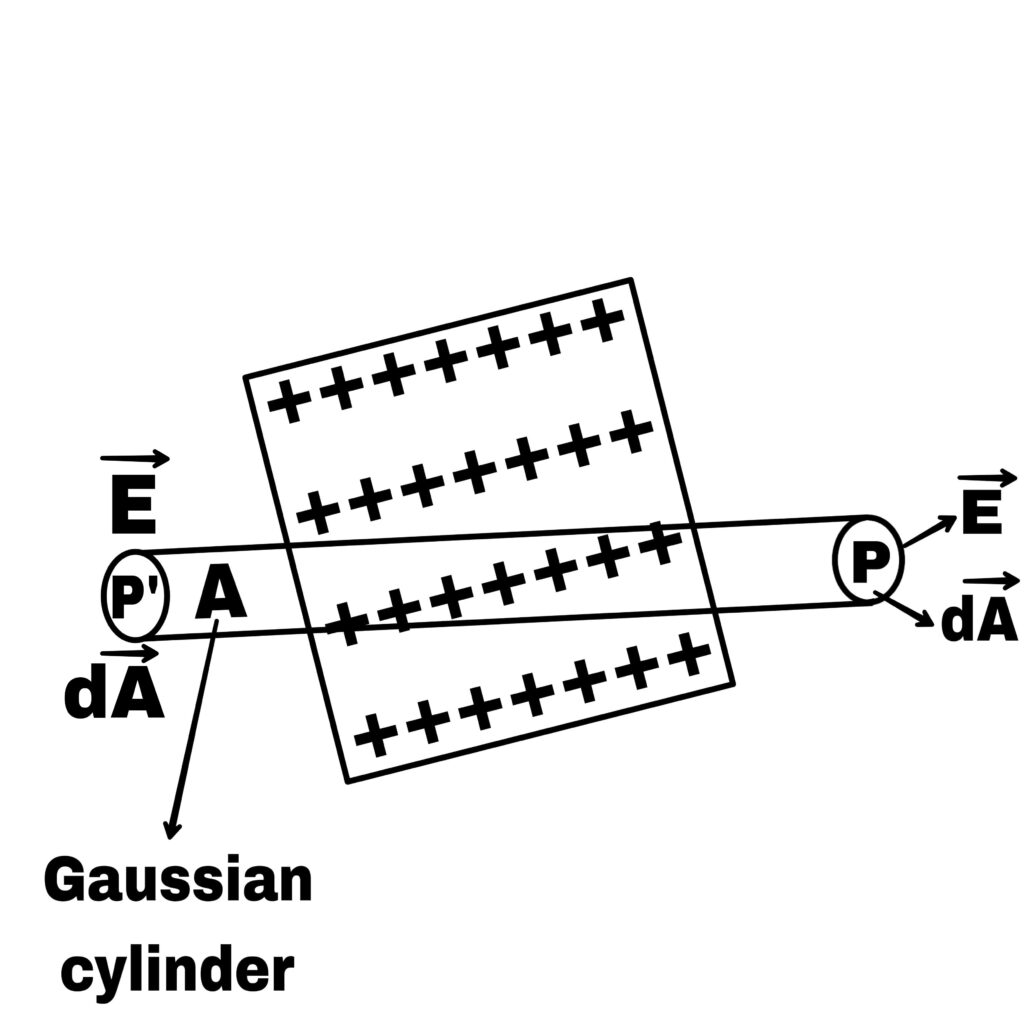
Suppose that on one surface of a uniformly charged flat sheet of infinite extension whose surface density is δ.
Near a positively charged flat sheet of infinite extension, there is a point P at a distance r from the sheet at which the electric field intensity is to be calculated.
Suppose that, point P’ is the intersection of point P on the other side of the sheet, We imagine a Gaussian cylinder across the sheet whose flat ends are parallel to the sheet and pass through points P and P’.
If area of each end of this cylinder is A, then electric flux passing through both ends of the cylinder is,
Φₑ=∫ₐ→E.→A+∫ₐ→E.→A
Φₑ=∫ₐE.dA.cos0°+∫ₐE.dA.cos0°
Φₑ=2∫ₐE.dA
Φₑ=2E∫ₐdA
Φₑ=2EA——-(1)
But by Gauss’s theorem,
Φₑ = q/∈₀
Where q= is the total charge enclosed by the Gaussian cylinder.
Hence,
q=δ.A (δ=q/A)
Φₑ = q/∈₀
Φₑ=δ.A/∈₀——-(2)
From equation (1) and (2)
2E.A=δ.A/∈₀
E=δ/2∈₀