Refraction of plane waves using Huygens’s theory
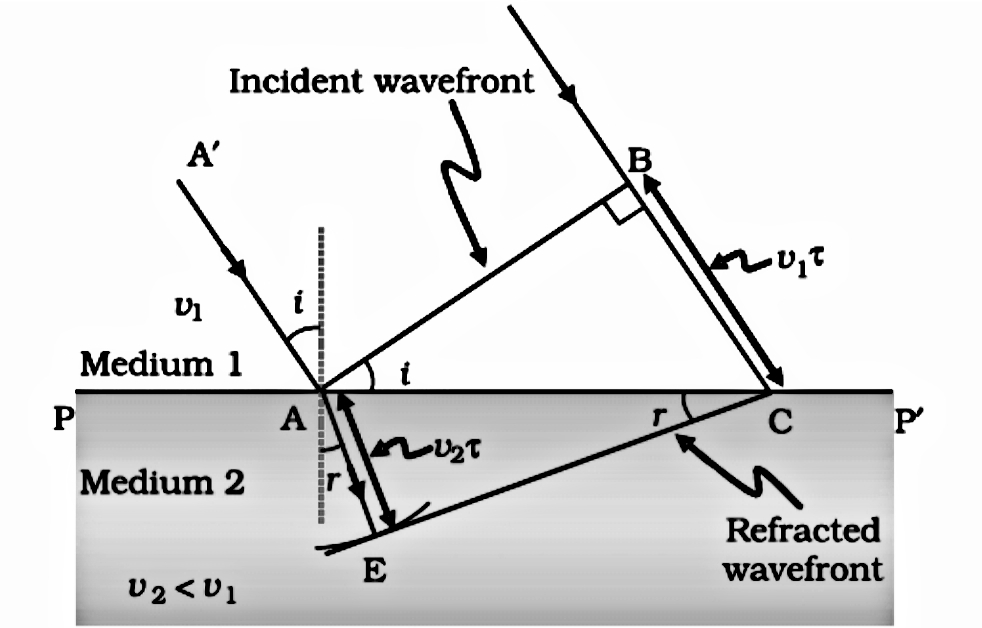
Let PP ‘is the surface separating mediums 1 and 2 and V1 and V2 are the time taken to cover the distance between the waveform and BC.
BC = V1t
AE = V2t∆
ABC and ∆AEC
Sini=BC/AC
Sinr=AE/AC
Sini=V1t/AC _______ (1)
Sinr=V2t/AC _______ (2)
Here i and r are the incidence and incidence angles of refraction respectively.
Sini/Sinr=V1t/V2t
Sini/Sinr=V1/V2
Therefore,
n1=C/V1,
n2=C/V2
n1 and n2 are the refractive indexes of mediums 1 and 2.
We know that
n1sini=n2sinr
sini/sinr=n2/n1
This is Snell’s law of refraction.
If λ1 and λ2 represent the wavelength of light in medium 1 and medium 2, respectively, and if the distance BC is equal to λ1 then the distance AE will be equal to λ2.
Therefore,
λ1 / λ2 = V1 / V2
Reflection of plane waves using Huygens’s theory
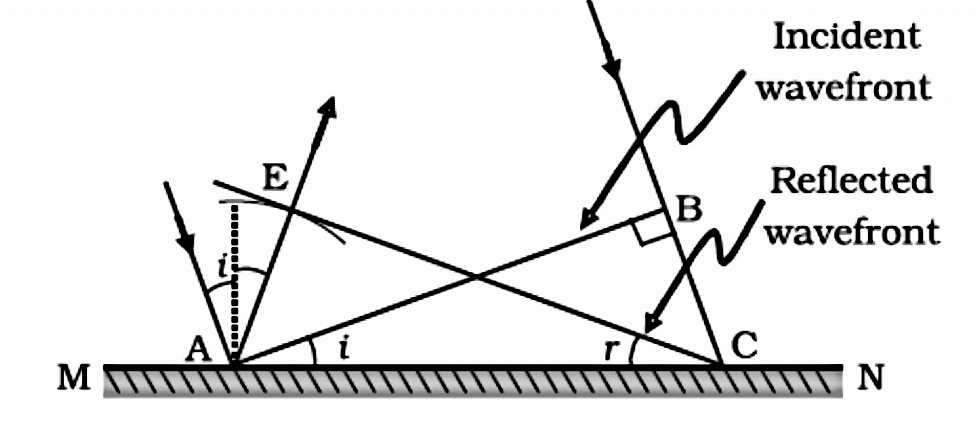
Now, on a reflective surface, MN is a plane wave AB incident at any angle i.
If v represents the speed of the wave in the medium and τ represents the time taken by the traverse to move from point B to C.
Then distance,
BC = vτ
Let the radius v point from point A to form the reflected waveform and CE represent the tangent plane drawn from point C on this sphere.
So,
AE = BC = vτ
From the triangles EAC and BAC we will find that these two are congruent.
The angle I and angler will be equal.
(This is the law of reflection.)
